��Ŀ����
13��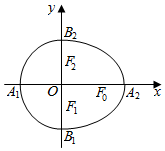 ���ǰ��ɰ���Բ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$��x��0�������Բ$\frac{{y}^{2}}{{b}^{2}}+\frac{{x}^{2}}{{c}^{2}}=1$��x��0���ϳɵ����߳�������Բ��������a2=b2+c2��a��0��b��c��0����ͼ����F0��F1��F2����Ӧ��Բ�Ľ��㣬A1��A2��B1��B2�ֱ��ǡ���Բ����x��y��Ľ��㣮
���ǰ��ɰ���Բ$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$��x��0�������Բ$\frac{{y}^{2}}{{b}^{2}}+\frac{{x}^{2}}{{c}^{2}}=1$��x��0���ϳɵ����߳�������Բ��������a2=b2+c2��a��0��b��c��0����ͼ����F0��F1��F2����Ӧ��Բ�Ľ��㣬A1��A2��B1��B2�ֱ��ǡ���Բ����x��y��Ľ��㣮��1������F0F1F2�DZ߳�Ϊ1�ĵȱ������Σ���Բ���ķ��̣�
��2����|A1A2|��|B1B2|ʱ����$\frac{b}{a}$��ȡֵ��Χ��
���� ��1����������F0F1F2�DZ߳�Ϊ1�ĵȱ������Σ��ó�a��b��c�Ĺ�ϵ�����a��b��c��ֵ�������ó�����Բ���ķ��̣�
��2����|A1A2|��|B1B2|�ɵ�a��b��c�IJ��ȹ�ϵʽ����c��a��b���棬�õ�����a��b�IJ���ʽ����ⲻ��ʽ�ô𰸣�
��� �⣺��1��������ɵã�F0��c��0����F1��0��-$\sqrt{{b}^{2}-{c}^{2}}$����F2��0��$\sqrt{{b}^{2}-{c}^{2}}$����
��|F0F1|=$\sqrt{��{b}^{2}-{c}^{2}��+{c}^{2}}$=b=1��|F1F2|=2$\sqrt{{b}^{2}-{c}^{2}}$=1��
��${c}^{2}=\frac{3}{4}$��${a}^{2}={b}^{2}+{c}^{2}=1+\frac{3}{4}=\frac{7}{4}$��
������Բ������Ϊ$\frac{4}{7}{x}^{2}+{y}^{2}=1$��x��0����${y}^{2}+\frac{4}{3}{x}^{2}=1$��x��0����
��2����|A1A2|��|B1B2|����a+c��2b��c��2b-a����$\sqrt{{a}^{2}-{b}^{2}}$��2b-a��
����ƽ����a2-b2����2b-a��2��
��$\frac{b}{a}��\frac{4}{5}$����b��c��
��b2��c2����b2��a2-b2��
��$\frac{{b}^{2}}{{a}^{2}}��\frac{1}{2}$����$\frac{b}{a}$$��\frac{\sqrt{2}}{2}$��
��$\frac{b}{a}$�ʣ�$\frac{\sqrt{2}}{2}��\frac{4}{5}$����
���� �������¶����⣬������Բ�ļ����ʣ�������ѧת��˼�뷽�������е��⣮

 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д� ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�| A�� | A⊆B | B�� | B⊆A | C�� | A��∁RB=R | D�� | A��B=∅ |
| A�� | k=2 | B�� | k=3 | C�� | .k=$\frac{1}{3}$��3 | D�� | k=2��$\frac{1}{2}$ |
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
| A�� | 12+13i | B�� | 13+12i | C�� | -13i | D�� | 13i |
| A�� | i | B�� | -i | C�� | 1 | D�� | -1 |
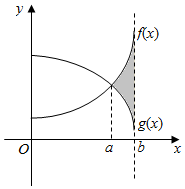 ��ͼ��ʾ����֪${��}_{0}^{b}$f��x��dx=11��${��}_{0}^{b}$g��x��dx=9��${��}_{0}^{a}$[g��x��-f��x��]dx=5����ͼ����Ӱ���ֵ����Ϊ7��
��ͼ��ʾ����֪${��}_{0}^{b}$f��x��dx=11��${��}_{0}^{b}$g��x��dx=9��${��}_{0}^{a}$[g��x��-f��x��]dx=5����ͼ����Ӱ���ֵ����Ϊ7��