题目内容
2. 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.(1)求证:平面MQB⊥平面PAD;
(2)若二面角M-BQ-C大小的为60°,求QM的长.
分析 (1)证明CD∥BQ,推出QB⊥AD.得到BQ⊥平面PAD,然后证明平面MQB⊥平面PAD.
(2)证明PQ⊥AD.推出PQ⊥平面ABCD,以Q为原点建立空间直角坐标系.求出相关点的坐标,求出平面MBQ法向量,平面BQC的法向量,然后利用利用空间向量的数量积求解即可.
解答 解:(1)∵AD∥BC,BC=$\frac{1}{2}$AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD∥BQ …(2分)
∵∠ADC=90°∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD且平面PAD∩平面ABCD=AD,
∴BQ⊥平面PAD.∵BQ?平面MQB,∴平面MQB⊥平面PAD…(5分)
(2)∵PA=PD,Q为AD的中点,∴PQ⊥AD.
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,∴PQ⊥平面ABCD.…(6分)
如图,以Q为原点建立空间直角坐标系.
则Q(0,0,0),A(1,0,0),P(0,0,$\sqrt{3}$),B(0,$\sqrt{3}$,0),C(-1,$\sqrt{3}$,0),
由 $\overrightarrow{PM}$=$λ\overrightarrow{PC}$=$λ(-1,\sqrt{3},-\sqrt{3})$,且0≤λ≤1,得M($-λ,\sqrt{3}λ,\sqrt{3}-\sqrt{3}λ$)
所以$\overrightarrow{QM}$=($-λ,\sqrt{3}λ,\sqrt{3}(1-λ)$),又$\overrightarrow{QB}$=(0,$\sqrt{3}$,0),
∴平面MBQ法向量为$\overrightarrow{m}$=($\sqrt{3},0,\frac{1-λ}{λ}$)…(8分)
由题意知平面BQC的法向量为$\overrightarrow{n}$=(0,0,1)…(9分)
∵二面角M-BQ-C为60°,
∴cos60°=$|\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}||\overrightarrow{m}|}|$=$\frac{1}{2}$,∴$λ=\frac{1}{2}$…(10分)
∴|QM|=$\frac{\sqrt{7}}{2}$…(12分)
点评 本题考查二面角的平面角的求法,平面与平面垂直的判定定理的应用,考查转化思想以及计算能力.

| A. | 甲 | B. | 乙 | C. | 丙 | D. | 不能确定 |
| x(万元) | 1 | 4 | 5 | 6 |
| y(百台) | 30 | 40 | 60 | 50 |
(1)已知这两个变量呈线性相关关系,试建立y与x之间的回归方程$\hat y=\hat bx+\hat a$;
(2)假如2017年该专卖店广告费用支出计划为10万元,请根据你得到的模型,预测这一年的销售量y.
参考公式:$\hat b=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
| A. | c<b<a | B. | c<a<b | C. | a<b<c | D. | a<c<b |
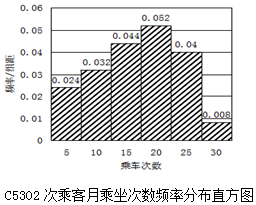 孝汉城铁于12月1日开通,C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了乘车次数的频率分布直方图和频数分布表.
孝汉城铁于12月1日开通,C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了乘车次数的频率分布直方图和频数分布表.C5321次乘客月乘坐次数频数分布表
| 乘车次数分组 | 频数 |
| [0,5) | 15 |
| [5,10) | 20 |
| [10,15) | 25 |
| [15,20) | 24 |
| [20,25) | 11 |
| [25,30] | 5 |
(2)已知在C5321次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成下面2×2列联表,并根据资料判断,是否有90%的把握认为年龄有乘车次数有关,说明理由.
| 老乘客 | 新乘客 | 合计 | |
| 50岁以上 | 10 | 25 | 35 |
| 50岁以下 | 30 | 35 | 65 |
| 合计 | 40 | 60 | 100 |
| P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
| A. | A∪B=A | B. | A∩B=A | C. | A=B | D. | (∁RA)∩B=∅ |