Question

14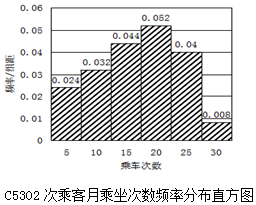．孝汉城铁于12月1日开通，C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况，分别在两个车次各随机抽取了100名旅客进行调查，下面是根据调查结果，绘制了乘车次数的频率分布直方图和频数分布表．
C5321次乘客月乘坐次数频数分布表

乘车次数分组	频数
[0，5）	15
[5，10）	20
[10，15）	25
[15，20）	24
[20，25）	11
[25，30]	5

（1）若将频率视为概率，月乘车次数不低于15次的称之为“老乘客”，试问：哪一车次的“老乘客”较多，简要说明理由．
（2）已知在C5321次列车随机抽到的50岁以上人员有35名，其中有10名是“老乘客”，由条件完成下面2×2列联表，并根据资料判断，是否有90%的把握认为年龄有乘车次数有关，说明理由．

	老乘客	新乘客	合计
50岁以上	10	25	35
50岁以下	30	35	65
合计	40	60	100

附：随机变量${k^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$（其中n=a+b+c+d为样本总量）

P（k2≥k0）	0.25	0.15	0.10	0.05	0.025
k0	1.323	2.072	2.706	3.841	5.024

Answer 1

分析 （1）根据题意，计算对应的频率值并比较大小即可；
（2）填写列联表，计算观测值，对照临界值表得出结论．

解答 解：（1）根据题意，C5302次“老乘客”的概率为
P₁=（0.052+0.04+0.008）×5=0.5，
C5321次“老乘客”的概率为：
${P_2}=\frac{24+11+5}{100}=0.4$，
∵P₁＞P₂，
∴5302次老乘客较多； （6分）
（2）填写列联表如下；

	老乘客	新乘客	合计
50岁以上	10	25	35
50岁以下	30	35	65
合计	40	60	100

计算观测值为k²=$\frac{100{×（10×35-25×30）}^{2}}{35×65×40×60}$≈2.93≥2.706，（10分）
对照临界值表得，有90%的把握认为年龄与乘车次数有关．          （12分）

点评 本题考查了频率分布直方图以及独立性检验的应用问题，是基础题目．