题目内容
5.甲、乙两人下棋,和棋的概率为$\frac{1}{2}$,乙获胜的概率为$\frac{1}{3}$,则甲获胜的概率和甲不输的概率分别为( )| A. | $\frac{1}{6}$,$\frac{1}{6}$ | B. | $\frac{1}{2}$,$\frac{2}{3}$ | C. | $\frac{1}{6}$,$\frac{2}{3}$ | D. | $\frac{2}{3}$,$\frac{1}{2}$ |
分析 利用对立事件概率计算公式求解.
解答 解:∵甲、乙两人下棋,和棋的概率为$\frac{1}{2}$,乙获胜的概率为$\frac{1}{3}$,
∴甲获胜的概率p1=1-$\frac{1}{2}-\frac{1}{3}$=$\frac{1}{6}$,
甲不输的概率${p}_{2}=1-\frac{1}{3}=\frac{2}{3}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
16.若x,y是正数,且$\frac{1}{x}$+$\frac{4}{y}$=1,则xy有( )
| A. | 最小值16 | B. | 最小值$\frac{1}{16}$ | C. | 最大值16 | D. | 最大值$\frac{1}{16}$ |
20.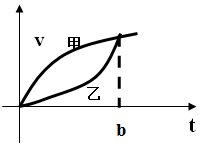 甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
 甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )| A. | a甲(b)>a乙(b),S甲(b)>S乙(b) | B. | a甲(b)<a乙(b),S甲(b)<S乙(b) | ||
| C. | a甲(b)<a乙(b),S甲(b)>S乙(b) | D. | a甲(b)<a乙(b),S甲(b)<S乙(b) |
10.若点P(m-2,n+1),Q(n,m-1)关于直线l对称,则l的方程是( )
| A. | x-y+1=0 | B. | x-y=0 | C. | x+y+1=0 | D. | x+y=0 |
15.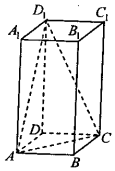 在正四棱柱ABCD-A1B1C1D1中,AB=2,BB1=4,则BB1与平面ACD1所成角的正弦值为( )
在正四棱柱ABCD-A1B1C1D1中,AB=2,BB1=4,则BB1与平面ACD1所成角的正弦值为( )
 在正四棱柱ABCD-A1B1C1D1中,AB=2,BB1=4,则BB1与平面ACD1所成角的正弦值为( )
在正四棱柱ABCD-A1B1C1D1中,AB=2,BB1=4,则BB1与平面ACD1所成角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
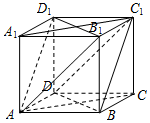 已知正方体ABCD-A1B1C1D1棱长为a.
已知正方体ABCD-A1B1C1D1棱长为a. 函数f(x)是R上的奇函数,且当x>0时,函数的解析式为f(x)=log2(x+1).
函数f(x)是R上的奇函数,且当x>0时,函数的解析式为f(x)=log2(x+1).