题目内容
15.函数y=Asin(ωx+ϕ)$(ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则函数表达式为( )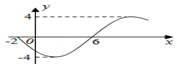
| A. | $y=-4sin(\frac{π}{8}x-\frac{π}{4})$ | B. | $y=4sin(\frac{π}{8}x-\frac{π}{4})$ | C. | $y=-4sin(\frac{π}{8}x+\frac{π}{4})$ | D. | $y=4sin(\frac{π}{8}x+\frac{π}{4})$ |
分析 观察函数的图象可得,函数的最小值-4,且在一周期内先出现最小值,所以A=-4,由图可得周期T=16,代入周期公式T=$\frac{2π}{ω}$可求ω;再把函数图象上的最值点代入结合已知φ的范围可得φ的值.
解答 解:由函数的图象可得最大值为4,且在一周期内先出现最小值,
所以A=-4
观察图象可得函数的周期T=16,ω=$\frac{2π}{16}$=$\frac{π}{8}$
又函数的图象过(2,-4)代入可得sin($\frac{π}{4}$+φ)=1
∴$\frac{π}{4}$+φ=$\frac{π}{2}$+2kπ
∵|φ|<$\frac{π}{2}$,∴φ=$\frac{π}{4}$
∴函数的表达式y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$).
故选C.
点评 1本题主要考查了由三角函数的图象求解函数的解析式,其步骤一般是:由函数的最值求解A,(但要判断是先出现最大值或是最小值,从而判断A的正负号)由周期求解ω,由函数图象上的点(一般用最值点)代入求解φ.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
3.已知椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$和圆${C_2}:{x^2}+{y^2}={b^2}$,若椭圆C1上存在点P,过点P作圆C2的两条切线PA,PB(A,B为对应的切点),且满足$∠APB=\frac{π}{3}$,则椭圆最圆的时离心率e=( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
4.半径不等的两定圆O1,O2没有公共点,且圆心不重合,动圆O与定圆O1和定圆O2都内切,则圆心O的轨迹是( )
| A. | 双曲线的一支 | B. | 椭圆 | ||
| C. | 双曲线的一支或椭圆 | D. | 双曲线或椭圆 |
5.已知随机变量ξ~B(5,$\frac{1}{3}$),则P(ξ=3)=( )
| A. | $\frac{5}{27}$ | B. | $\frac{7}{81}$ | C. | $\frac{40}{243}$ | D. | $\frac{19}{144}$ |
 如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图,ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.