Question

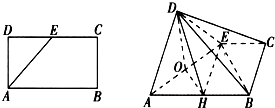已知矩形ABCD中，AB=2AD=4，E为CD的中点，沿AE将三角形AED折起，使DB=2

3

，如图，O、H分别为AE、AB的中点．
（1）求证：直线OH∥平面BDE；
（2）求证：平面ADE⊥平面ABCE；
（3）求二面角O-DH-E的余弦值的大小．

Answer 1

考点：二面角的平面角及求法,直线与平面平行的判定,平面与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（1）直接利用线线平行得到线面平行．
（2）利用相关的运算求出相关的线段长，利用勾股定理的逆定理求出线面垂直，再转化成面面垂直．
（3）先做出二面角的平面角，再利用余弦定理求出结果．

解答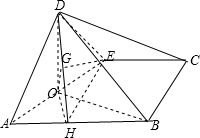： （1）证明：已知矩形ABCD中，E为CD的中点，沿AE将三角形AED折起，使DB=2

3

，如图，O、H分别为AE、AB的中点．
所以：OH∥BE
OH?平面BDE，BE?平面BDE
所以：直线OH∥平面BDE
（2）在矩形ABCD中，AB=2AD=4，E为CD的中点，O、H分别为AE、AB的中点．
所以：OD⊥AE，OD=

2

连接OB，利用余弦定理解得：
OB²=AO²+AB²-2AO•ABcos∠OAB
解得：OB=

10

所以：OD²+OB²=BD²
即：OD⊥OB
OD⊥平面ABCE
OD?平面ADE
所以：平面ADE⊥平面ABCE
（3）如图所示：OD=OH=

2

，DE=HE=2，
做DH的中点G，连接OG，GE
所以：OG⊥DH，GE⊥DH
即：∠OGE即为二面角O-DH-E的平面角．
所以进一步解得：OD=OH=

2

，
利用（2）的结论进一步求得：DH=2，所以OG=1，进一步得：
△DEH为等边三角形．
利用余弦定理得：cos∠OGE=

3

3

即：二面角O-DH-E的余弦值为

3

3

点评：本题考查的知识要点：线面平行的判定定理，面面垂直的判定定理，二面角的求法及应用，相关的运算问题．属于基础题型．