题目内容
已知数列{an}的前n项和为Sn,且an+Sn=4.
(1)求数列{an}的通项公式;
(2)是否存在正整数k,使
>2成立.
(1)求数列{an}的通项公式;
(2)是否存在正整数k,使
| Sk+1-2 |
| Sk-2 |
考点:数列与函数的综合
专题:等差数列与等比数列
分析:(1)由已知得an+1=
an,a1=2.由此能求出an=2×(
)n-1.
(2)由(1)知Sn=
=4[1-(
)n],
>2等价于
>2,由此能推导出不存在这样的k,使不等式
>2成立.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)知Sn=
2(1-
| ||
1-
|
| 1 |
| 2 |
| Sk+1-2 |
| Sk-2 |
| 4-21-k-2 |
| 4-22-k-2 |
| Sk+1-2 |
| Sk-2 |
解答:
解:(1)由题意,an+Sn=4,an+1+Sn+1=4,
两式相减得an+1=
an,
当n=1时,a1+S1=2a1=4,
得a1=2.
∴数列{an}是以首项a1=2,公比为q=
的等比数列.
∴an=2×(
)n-1.
(2)由(1)知Sn=
=4[1-(
)n],
∴
>2等价于
>2,
∴
<0,
∴
<21-k<1,
∴1<2k-1<
,
∵k是正整数,
∴2k-1正整数,这与1<2k-1<
相矛盾,
故不存在这样的k,使不等式成立.
两式相减得an+1=
| 1 |
| 2 |
当n=1时,a1+S1=2a1=4,
得a1=2.
∴数列{an}是以首项a1=2,公比为q=
| 1 |
| 2 |
∴an=2×(
| 1 |
| 2 |
(2)由(1)知Sn=
2(1-
| ||
1-
|
| 1 |
| 2 |
∴
| Sk+1-2 |
| Sk-2 |
| 4-21-k-2 |
| 4-22-k-2 |
∴
| 3-21-k-2 |
| 3-21-k-2 |
∴
| 2 |
| 3 |
∴1<2k-1<
| 3 |
| 2 |
∵k是正整数,
∴2k-1正整数,这与1<2k-1<
| 3 |
| 2 |
故不存在这样的k,使不等式成立.
点评:本题考查数列的通项公式的求法,考查满足条件的实数k的值是否成立的判断与求法,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
相关题目
已知任意向量
,
及实数λ,那么“λ
+
=0”成立是“
∥
”成立的( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、非充分必要条件 |
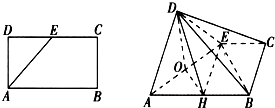 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将三角形AED折起,使DB=2
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将三角形AED折起,使DB=2