题目内容
关于x的不等式mx-n>0的解集为(-∞,3),则关于x的不等式
>0的解集为 .
| mx+n |
| x-2 |
考点:其他不等式的解法
专题:计算题,不等式的解法及应用
分析:由于x的不等式mx-n>0的解集为(-∞,3),则3为方程mx-n=0(m<0)的根.即有n=3m,代入所求不等式,化简整理,转化为一次不等式组,解得即可.
解答:
解:由于x的不等式mx-n>0的解集为(-∞,3),
则3为方程mx-n=0(m<0)的根.
即有n=3m,
则关于x的不等式
>0即为
<0,
即有
或
解得,-3<x<2或x∈∅,
则解集为(-3,2).
故答案为:(-3,2).
则3为方程mx-n=0(m<0)的根.
即有n=3m,
则关于x的不等式
| mx+n |
| x-2 |
| x+3 |
| x-2 |
即有
|
|
解得,-3<x<2或x∈∅,
则解集为(-3,2).
故答案为:(-3,2).
点评:本题考查一次不等式的解法和分式不等式的解法,考查运算能力,属于基础题.

练习册系列答案
相关题目
定义运算
=
,称
=
为将点(x,y)映到点(x′,y′)的一次变换.若
=
把直线y=x上的各点映到这点本身,而把直线y=3x上的各点映到这点关于原点对称的点.则p,q的值分别是( )
|
|
|
|
|
|
|
|
| A、p=1,q=1 |
| B、p=3,q=1 |
| C、p=3,q=3 |
| D、p=3,q=-2 |
已知任意向量
,
及实数λ,那么“λ
+
=0”成立是“
∥
”成立的( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充分必要条件 |
| D、非充分必要条件 |
函数y=
的图象与函数y=2sinπx,(-2≤x≤4)的图象所有交点的横坐标之和等于( )
| 1 |
| 1-x |
| A、8 | B、6 | C、4 | D、2 |
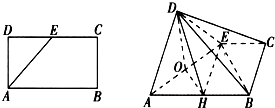 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将三角形AED折起,使DB=2
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将三角形AED折起,使DB=2