题目内容
 如图,在四棱锥S-ABCD中,底面ABCD是正方形,且SA=SB=SC=SD,SO是这个三棱锥的高,SM垂直于BC,垂足为M,若SO=8,SM=10.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,且SA=SB=SC=SD,SO是这个三棱锥的高,SM垂直于BC,垂足为M,若SO=8,SM=10.(1)求侧棱长;
(2)求该四棱锥的侧面积.
考点:棱柱、棱锥、棱台的侧面积和表面积,棱锥的结构特征
专题:空间位置关系与距离
分析:(1)根据;Rt△SOM中,Rt△SBM中求解.
(2)判断出此四棱锥为正三棱锥,底面边长为BC=12,即可求解得出4×
×BC×SM.
(2)判断出此四棱锥为正三棱锥,底面边长为BC=12,即可求解得出4×
| 1 |
| 2 |
解答:
解:(1) 连接OM,根据题意得出;Rt△SOM中,SO=8,SM=10.
连接OM,根据题意得出;Rt△SOM中,SO=8,SM=10.
∴OM=
=
=6,
∴BM=6,
∵Rt△SBM中,BM=6,SM=10.
∴SB=
=
=
,
故侧棱长:
,
(2)∵在四棱锥S-ABCD中,底面ABCD是正方形,且SA=SB=SC=SD,
∴此四棱锥为正三棱锥,底面边长为BC=12,
∴该四棱锥的侧面积=4×
×BC×SM=4×
×12×10=240,.
 连接OM,根据题意得出;Rt△SOM中,SO=8,SM=10.
连接OM,根据题意得出;Rt△SOM中,SO=8,SM=10.∴OM=
| SM2-SO2 |
| 100-64 |
∴BM=6,
∵Rt△SBM中,BM=6,SM=10.
∴SB=
| SM2+BM2 |
| 100+36 |
| 136 |
故侧棱长:
| 136 |
(2)∵在四棱锥S-ABCD中,底面ABCD是正方形,且SA=SB=SC=SD,
∴此四棱锥为正三棱锥,底面边长为BC=12,
∴该四棱锥的侧面积=4×
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了空间几何体的性质,运用求解边长,斜高问题,属于计算题,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=
lg(1-x)的定义域为( )
| x |
| A、[0,1) |
| B、(0,1) |
| C、(0,1] |
| D、[0,1] |
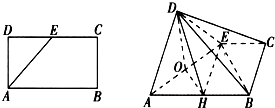 已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将三角形AED折起,使DB=2
已知矩形ABCD中,AB=2AD=4,E为CD的中点,沿AE将三角形AED折起,使DB=2