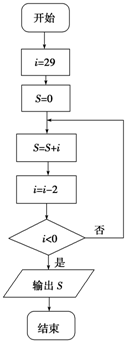
题目内容
方程2x=x2的根有 个．
考点：函数的零点与方程根的关系
专题：函数的性质及应用
分析：根据方程和函数关系将方程转化为两个函数，然后利用数形结合即可得到结论．
解答：
解：∵2x=x2，
设f（x）
=2x，g（x）=x2，
作出两个函数的图象如图：由图象可知两个函数的交点为3个，
即方程根的公式为3个．
当x＜0时，有一个根，
当x=2或x=4时，也是方程的根，
故答案为：3．
设f（x）
=2x，g（x）=x2，作出两个函数的图象如图：由图象可知两个函数的交点为3个，
即方程根的公式为3个．
当x＜0时，有一个根，
当x=2或x=4时，也是方程的根，
故答案为：3．
点评：本题主要考查方程根的个数的判断，利用函数和方程之间的关系将条件进行转化，利用数形结合是解决本题的关键，注意作图的准确性．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
已知函数y=f（x）（x∈R），g（x）=f（x）+2x（x∈R），则函数f（x）在R上递增是g（x）在R上递增的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
b=0是函数f（x）=x2+bx+c为偶函数的（ ）条件．
| A、充分而不必要 |
| B、必要而不充分 |
| C、充分必要 |
| D、既不充分也不必要 |