题目内容
已知函数y=f(x)(x∈R),g(x)=f(x)+2x(x∈R),则函数f(x)在R上递增是g(x)在R上递增的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据函数单调性的性质,以及充分条件和必要条件的定义进行判断即可.
解答:
解:若f(x)在R上递增,则根据函数单调性的性质可知g(x)=f(x)+2x单调递增.
若f(x)=-x,此时g(x)=f(x)+2x=-x+2x=x单调递增,但f(x)=-x不是增函数,
∴函数f(x)在R上递增是g(x)在R上递增的充分不必要条件,
故选:A.
若f(x)=-x,此时g(x)=f(x)+2x=-x+2x=x单调递增,但f(x)=-x不是增函数,
∴函数f(x)在R上递增是g(x)在R上递增的充分不必要条件,
故选:A.
点评:本题主要考查充分条件和必要条件的应用,利用函数单调性的性质是解决本题的关键.

练习册系列答案
相关题目
已知a=log45,b=4-
,c=sin2,则a、b、c的大小关系是( )
| 1 |
| 2 |
| A、b<c<a |
| B、c<a<b |
| C、a<b<c |
| D、c<b<a |
下列各式中,求导运算正确的是( )
| A、(uv)′=u′v′ | ||||
B、(
| ||||
| C、(uv)′=uv+u′v′ | ||||
D、(
|
已知角θ为第四象限角,且tanθ=-
,则sinθ+cosθ=( )
| 3 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
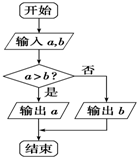 如图所示的程序框图,其功能是( )
如图所示的程序框图,其功能是( )| A、输入a,b的值,按从小到大的顺序输出它们的值 |
| B、输入a,b的值,按从大到小的顺序输出它们的值 |
| C、求a,b的最大值 |
| D、求a,b的最小值 |

 如图,ABCD为正四面体,AD⊥面α于点A,点B、C、D均在平面α外,且在平面α的同一侧,线段BC的中点为E,则直线AE与平面α所成角的正弦值为( )
如图,ABCD为正四面体,AD⊥面α于点A,点B、C、D均在平面α外,且在平面α的同一侧,线段BC的中点为E,则直线AE与平面α所成角的正弦值为( )