题目内容
b=0是函数f（x）=x2+bx+c为偶函数的（ ）条件．
| A、充分而不必要 |
| B、必要而不充分 |
| C、充分必要 |
| D、既不充分也不必要 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据函数奇偶性的定义和性质，以及充分条件和必要条件的定义进行判断即可．
解答：
解：b=0时，f（x）=x2+bx+c=x2+c为偶函数．
若f（x）=x2+bx+c为偶函数，则f（-x）=x2-bx+c=x2+bx+c，
即-bx=bx，
∴-b=b，解得b=0．
b=0是函数f（x）=x2+bx+c为偶函数的充分必要条件．
故选：C．
若f（x）=x2+bx+c为偶函数，则f（-x）=x2-bx+c=x2+bx+c，
即-bx=bx，
∴-b=b，解得b=0．
b=0是函数f（x）=x2+bx+c为偶函数的充分必要条件．
故选：C．
点评：本题主要考查充分条件和必要条件的应用，利用偶函数的定义是解决本题的关键．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知角θ为第四象限角，且tanθ=-
，则sinθ+cosθ=（ ）
| 3 |
| 4 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
圆心在直线y=-4x上，且与直线l：x+y-1=0相切于点P（3，-2）的圆的方程是（ ）
| A、（x-1）2+（y+4）2=8 |
| B、（x-3）2+（y-1）2=9 |
| C、（x+1）2+（y-3）2=5 |
| D、（x-1）2+（y-5）2=16 |
如图程序，输出的结果A是（ ）
| A、5 | B、6 | C、15 | D、120 |
在△ABC中，边a，b，c的对角分别为A，B，C，若a2=b2+c2+
bc，则A的大小为（ ）
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
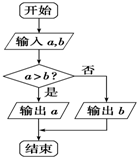如图所示的程序框图，其功能是（ ）| A、输入a，b的值，按从小到大的顺序输出它们的值 |
| B、输入a，b的值，按从大到小的顺序输出它们的值 |
| C、求a，b的最大值 |
| D、求a，b的最小值 |
学校体育场南侧有4个大门，北侧有3个大门，西侧有2个大门，某学生到该体育场训练，但必须是从南或北门进入，从西门或北门出去，则他进出门的方案有（ ）
| A、7个 | B、12个 |
| C、24个 | D、35个 |