题目内容
6.设f(x)满足:①任意x∈R,有f(x)+f(2-x)=0;②当x≥1时,f(x)=|x-a|-1,(a>0),若x∈R,恒有f(x)>f(x-m),则m的取值范围是( )| A. | (0,+∞) | B. | (4,+∞) | C. | (3,+∞) | D. | (5,+∞) |
分析 根据函数的对称性求出a的值,作出函数f(x)的图象,利用数形结合以及图象关系进行平移计算即可.
解答 解:∵任意x∈R,有f(x)+f(2-x)=0,
∴f(2-x)=-f(x),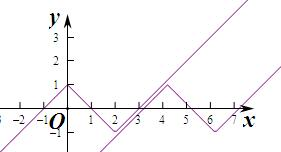
则函数关于(1,0)点对称,
当x=1时,f(1)+f(2-1)=0,即2f(1)=0,
则f(1)=0,
∵当x≥1时,f(x)=|x-a|-1,
∴f(1)=|1-a|-1=0,
则|a-1|=1,则a-1=1或a-1=-1,
则a=2或a=0,
∵a>0,
∴a=2,
即当x≥1时,f(x)=|x-2|-1
当x≤1时,-x≥-1,2-x≥1,
即f(x)=-f(2-x)=-(|2-x-2|-1)=1-|x|,x≤1,
作出函数f(x)的图象如图:
若f(x)>f(x-m),则由图象知,将函数f(x)向右平移m个单位即可,
由图象知,m>4,
故选:B
点评 本题主要考查函数图象的应用,根据函数的对称性求出函数的解析式,以及利用图象平移是解决本题的关键.综合性较强,有一定的难度.

练习册系列答案
相关题目
7.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,x≤0}\\{lo{g}_{2}x,x>0}\end{array}\right.$,则函数y=f(x)的零点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
14.已知复数$z=\frac{10}{3+i}-2i$,其中i是虚数单位,则|z|=( )
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
16. 将一个圆的八个等分点分成相间的两组,连接每组的四个点得到两个正方形.去掉两个正方形内部的八条线段后可以形成一正八角星,如图所示.设正八角星的中心为O,并且 $\overrightarrow{OA}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{OB}$=$\overrightarrow{{e}_{2}}$,若将点O到正八角星16个顶点的向量,都写成为λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$,λ,μ∈R的形式,则λ+μ的最大值为( )
将一个圆的八个等分点分成相间的两组,连接每组的四个点得到两个正方形.去掉两个正方形内部的八条线段后可以形成一正八角星,如图所示.设正八角星的中心为O,并且 $\overrightarrow{OA}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{OB}$=$\overrightarrow{{e}_{2}}$,若将点O到正八角星16个顶点的向量,都写成为λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$,λ,μ∈R的形式,则λ+μ的最大值为( )
 将一个圆的八个等分点分成相间的两组,连接每组的四个点得到两个正方形.去掉两个正方形内部的八条线段后可以形成一正八角星,如图所示.设正八角星的中心为O,并且 $\overrightarrow{OA}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{OB}$=$\overrightarrow{{e}_{2}}$,若将点O到正八角星16个顶点的向量,都写成为λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$,λ,μ∈R的形式,则λ+μ的最大值为( )
将一个圆的八个等分点分成相间的两组,连接每组的四个点得到两个正方形.去掉两个正方形内部的八条线段后可以形成一正八角星,如图所示.设正八角星的中心为O,并且 $\overrightarrow{OA}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{OB}$=$\overrightarrow{{e}_{2}}$,若将点O到正八角星16个顶点的向量,都写成为λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$,λ,μ∈R的形式,则λ+μ的最大值为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 1+$\sqrt{2}$ | D. | 2$\sqrt{2}$ |