题目内容
1.在Rt△ABC中,∠A=90°,AB=AC=2,点D为AC中点,点E满足$\overrightarrow{BE}=\frac{1}{3}\overrightarrow{BC}$,则$\overrightarrow{AE}•\overrightarrow{BD}$=-2.分析 由已知画出图形,结合向量的加法与减法法则把$\overrightarrow{AE}、\overrightarrow{BD}$用$\overrightarrow{AB}、\overrightarrow{AC}$表示,展开$\overrightarrow{AE}•\overrightarrow{BD}$后代值得答案.
解答 解:如图,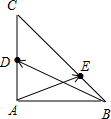
∵$\overrightarrow{BE}=\frac{1}{3}\overrightarrow{BC}$,
∴$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BE}=\overrightarrow{AB}+\frac{1}{3}\overrightarrow{BC}$=$\overrightarrow{AB}+\frac{1}{3}(\overrightarrow{AC}-\overrightarrow{AB})=\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$,
又D为AC中点,
∴$\overrightarrow{BD}=\overrightarrow{AD}-\overrightarrow{AB}=\frac{1}{2}\overrightarrow{AC}-\overrightarrow{AB}$,
则$\overrightarrow{AE}•\overrightarrow{BD}$=$(\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC})•(\frac{1}{2}\overrightarrow{AC}-\overrightarrow{AB})$=$\frac{1}{6}{\overrightarrow{AC}}^{2}-\frac{2}{3}{\overrightarrow{AB}}^{2}$=$(\frac{1}{6}-\frac{2}{3})×4=-2$.
故答案为:-2.
点评 本题考查平面向量的数量积运算,考查向量的加法与减法法则,是中档题.

 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案| A. | [2,+∞) | B. | (2,+∞) | C. | [$\sqrt{3}$,+∞) | D. | (-$\sqrt{3}$,+∞) |
| A. | (0,+∞) | B. | (4,+∞) | C. | (3,+∞) | D. | (5,+∞) |
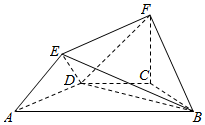 如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,若CB=CD=CF=a.
如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,若CB=CD=CF=a. 如图,在三棱锥A-BCD中,AB=AC=AD=BC=CD=4,BD=4$\sqrt{2}$,E,F分别为AC,CD的中点,G为线段BD上一点,且BE∥平面AGF.
如图,在三棱锥A-BCD中,AB=AC=AD=BC=CD=4,BD=4$\sqrt{2}$,E,F分别为AC,CD的中点,G为线段BD上一点,且BE∥平面AGF.