题目内容
8.设函数f(x)=$\frac{{a{x^3}}}{3}-b{x^2}+{a^2}x-\frac{1}{3}$在x=1处取得极值为0,则a+b=-$\frac{7}{9}$.分析 求出导函数,根据定义可知f'(1)=a-2b+a2=0,f(1)=0,得出a=1或a=-$\frac{2}{3}$,由极值概念可知a=1不成立,故a=-$\frac{2}{3}$,b=-$\frac{1}{9}$,得出答案.
解答 解:∵f(x)=$\frac{{a{x^3}}}{3}-b{x^2}+{a^2}x-\frac{1}{3}$,
∴f'(x)=ax2-2bx+a2,
∵在x=1处取得极值为0,
∴f'(1)=a-2b+a2=0,
f(1)=0,
∴a=1或a=-$\frac{2}{3}$,
∵函数有极值,a=1不成立.
∴a=-$\frac{2}{3}$,b=-$\frac{1}{9}$,
故答案为-$\frac{7}{9}$.
点评 本题考查了极值的概念和导函数的应用,属于基础题型,应熟练掌握.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知某口袋中有3个白球和a个黑球(a∈N*),现从中随机取出一球,再换回一个不同颜色的球(即若取出的是白球,则放回一个黑球;若取出的是黑球,则放回一个白球),记换好球后袋中白球的个数是ξ.若Eξ=3,则Dξ=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
17.随着“全面二孩”政策推行,我市将迎来生育高峰,今年新春伊始,各医院产科就已经一片忙碌,至今热度不减,卫生部门进行调查统计,期间发现各医院的新生儿中,不少都是“二孩”,在人民医院,共有50个宝宝降生,其中25个是“二孩”宝宝;博爱医院共有30个宝宝降生,其中10个是“二孩”宝宝.
(1)根据以上数据,完成下面的2×2列联表,并判断是否有90%的把握认为一孩或二孩宝宝的出生与医院有关?
(2)从两个医院当前出生的所有宝宝中按分层抽样方法抽取8个宝宝做健康咨询,若从这8个宝宝抽取两个宝宝进行体检.求这两个宝宝恰好都是来自人民医院的概率.
附:${K^2}=\frac{{n{{({αb-bc})}^2}}}{{({α+b})({c+d})({α+c})({b+d})}}$
(1)根据以上数据,完成下面的2×2列联表,并判断是否有90%的把握认为一孩或二孩宝宝的出生与医院有关?
| 一孩 | 二孩 | 合计 | |
| 人民医院 | |||
| 博爱医院 | |||
| 合计 |
附:${K^2}=\frac{{n{{({αb-bc})}^2}}}{{({α+b})({c+d})({α+c})({b+d})}}$
| P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 |
18.已知一个圆锥底面半径为1,母线长为3,则该圆锥内切球的表面积为( )
| A. | π | B. | $\frac{3π}{2}$ | C. | 2π | D. | 3π |
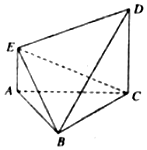 如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.
如图,△ABC为边长为2的正三角形,AE∥CD,且AE⊥平面ABC,2AE=CD=2.