题目内容
17.随着“全面二孩”政策推行,我市将迎来生育高峰,今年新春伊始,各医院产科就已经一片忙碌,至今热度不减,卫生部门进行调查统计,期间发现各医院的新生儿中,不少都是“二孩”,在人民医院,共有50个宝宝降生,其中25个是“二孩”宝宝;博爱医院共有30个宝宝降生,其中10个是“二孩”宝宝.(1)根据以上数据,完成下面的2×2列联表,并判断是否有90%的把握认为一孩或二孩宝宝的出生与医院有关?
| 一孩 | 二孩 | 合计 | |
| 人民医院 | |||
| 博爱医院 | |||
| 合计 |
附:${K^2}=\frac{{n{{({αb-bc})}^2}}}{{({α+b})({c+d})({α+c})({b+d})}}$
| P(k2>k0) | 0.4 | 0.25 | 0.15 | 0.10 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 |
分析 (1)计算K2,与2.072比较大小得出结论.
(2)从两个医院当前出生的所有宝宝中按分层抽样方法抽取8个宝宝做健康咨询,人民医院5人,博爱医院3人,确定基本事件的情况,即可求出概率.
解答 解:(1)
| 一孩 | 二孩 | 合计 | |
| 人民医院 | 25 | 25 | 50 |
| 博爱医院 | 20 | 10 | 30 |
| 合计 | 45 | 35 | 80 |
故没有90%的把握认为一孩或二孩宝宝的出生与医院有关.
(2)从两个医院当前出生的所有宝宝中按分层抽样方法抽取8个宝宝做健康咨询,人民医院5人,博爱医院3人,从这8个宝宝抽取两个宝宝进行体检,有${C}_{8}^{2}$=28种,这两个宝宝恰好都是来自人民医院,有${C}_{5}^{2}$=10种,所以这两个宝宝恰好都是来自人民医院的概率P=$\frac{10}{28}$=$\frac{5}{14}$.
点评 本题考查了分层抽样原理,古典概型的概率计算,独立检验的统计思想,属于基础题.

练习册系列答案
相关题目
12.某一算法框图如图所示,则输出的S值为( )
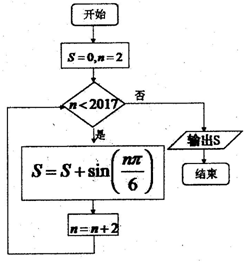

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
2.已知双曲线C:$\frac{x^2}{{a{\;}^2}}-\frac{y^2}{{b{\;}^2}}$=1的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某一条渐近线交于两点P,Q,若∠PAQ=$\frac{π}{3}$且$\overrightarrow{OQ}=5\overrightarrow{OP}$,则双曲线C的离心率为( )
| A. | 2 | B. | $\frac{{\sqrt{21}}}{3}$ | C. | $\frac{{\sqrt{7}}}{2}$ | D. | 3 |
6.已知$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,则$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
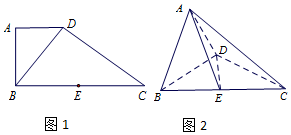 如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体
如图1,在直角梯形ABCD中,AD∥BC,AB⊥BC,BD⊥DC,点E是BC 边的中点,将△ABD沿BD折起,使平面ABD⊥平面BCD,连接AE,AC,DE,得到如图2所示的几何体