题目内容
已知函数f(x)=sin(
+x)cos(
-x),给出下列四个说法:
①若f(x1)=-f(x2),则x1=-x2; ②f(x)的最小正周期是2π;
③f(x)在区间[-
,
]上是增函数; ④f(x)的图象关于直线x=
对称.
其中正确说法的个数为( )
| π |
| 2 |
| π |
| 2 |
①若f(x1)=-f(x2),则x1=-x2; ②f(x)的最小正周期是2π;
③f(x)在区间[-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
其中正确说法的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:三角函数的化简求值,运用诱导公式化简求值
专题:三角函数的图像与性质
分析:化简解析式可得f(x)=
sin2x,由已知可求x1=-x2+2kπ(k∈Z),即可判断①错;
由周期公式可求f(x)的最小正周期是π,即可判断②错;
令-
+2kπ≤2x≤
+2kπ,可求得单调递增区间即可判断③对;
令2x=
+kπ,求得对称轴方程即可判断④对.
| 1 |
| 2 |
由周期公式可求f(x)的最小正周期是π,即可判断②错;
令-
| π |
| 2 |
| π |
| 2 |
令2x=
| π |
| 2 |
解答:
解:f(x)=sin(
+x)cos(
-x)=
sin2x,若f(x1)=-f(x2),则f(x1)=f(-x2),所以x1=-x2+2kπ(k∈Z),故①错;
f(x)的最小正周期是π,故②错;
令-
+2kπ≤2x≤
+2kπ,所以-
+kπ≤x≤
+kπ(k∈Z),故③对;
令2x=
+kπ,所以x=
+
(k∈Z),所以④对.
综上,正确说法的个数为2.
故选:B.
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
f(x)的最小正周期是π,故②错;
令-
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
令2x=
| π |
| 2 |
| π |
| 4 |
| kπ |
| 2 |
综上,正确说法的个数为2.
故选:B.
点评:本题主要考查了三角函数的化简求值,运用诱导公式化简求值,三角函数的图象与性质,属于基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
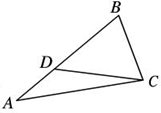 如图,D是△ABC的边AB的三等分点,则向量
如图,D是△ABC的边AB的三等分点,则向量| CD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知在xoy平面内有一区域M,命题甲:点(a,b)∈{(x,y||x-1|+|y-2|<2)};命题乙:点(a,b)∈M,如果甲是乙的必要条件,那么区域M的面积有( )
| A、最小值8 | B、最大值8 |
| C、最小值4 | D、最大值4 |
设α,β,γ为平面,m,n为直线,则m⊥β的一个充分条件是( )
| A、α⊥β,α∩β=n,m⊥n |
| B、α∩γ=m,α⊥γ,β⊥γ |
| C、α⊥β,β⊥γ,m⊥α |
| D、n⊥α,n⊥β,m⊥α |
已知函数f(x)=
,g(x)=x3,则f(x)•g(x)的奇偶性为( )
|
| A、是奇函数不是偶函数 |
| B、是偶函数不是奇函数 |
| C、是奇函数也是偶函数 |
| D、不是奇函数也不是偶函数 |
复数
(-2-i)+
的虚部是( )
| 1 |
| 5 |
| 1 |
| 1-2i |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
已知集合M={x|-2≤x<2},集合N={x|x2-2x-3≥0},则M∩N等于( )
| A、[-1,1] |
| B、[1,2) |
| C、[-2,-1] |
| D、[1,2) |
已知直线m和平面α,β,则下列四个命题中正确的是( )
| A、若α⊥β,m?β,则m⊥α |
| B、若α∥β,m∥α,则m∥β |
| C、若α∥β,m⊥α,则m⊥β |
| D、若m∥α,m∥β,则α∥β |