题目内容
设命题P:点A(sinα,cosα)与B(a2,2)在直线x+y-
=0的两侧,命题Q:函数f(x)=ln|x|在(-∞,0)上单调递减,则下列命题是真命题的是 .
①¬P; ②P∨Q; ③P∧Q.
| 3 |
①¬P; ②P∨Q; ③P∧Q.
考点:复合命题的真假
专题:简易逻辑
分析:先判断命题P,Q的真假,再利用复合命题真假的判断方法即可得出.
解答:
解:∵命题P:点A(sinα,cosα)与B(a2,2)在直线x+y-
=0的两侧,
∴(sinα+cosα-
)(a2+2-
)<0.
∵sinα+cosα-
=
sin(α+
)-
<
-
<0,a2+2-
>0,因此命题P是真命题.
命题Q:函数f(x)=ln|x|在(-∞,0)上单调递减,是真命题.
由此可得:①¬P是假命题;
②P∨Q是真命题;
③P∧Q是真命题.
故答案为:②③.
| 3 |
∴(sinα+cosα-
| 3 |
| 3 |
∵sinα+cosα-
| 3 |
| 2 |
| π |
| 4 |
| 3 |
| 2 |
| 3 |
| 3 |
命题Q:函数f(x)=ln|x|在(-∞,0)上单调递减,是真命题.
由此可得:①¬P是假命题;
②P∨Q是真命题;
③P∧Q是真命题.
故答案为:②③.
点评:本题考查了线性规划有关问题、复合函数的单调性、简易逻辑,考查了推理能力,属于基础题.

练习册系列答案
相关题目
已知x,y∈R,i为虚数单位,且x+yi=
,则x+y=( )
| 3+4i |
| 1+2i |
A、
| ||
B、
| ||
C、
| ||
D、
|
若△ABC与△BDC同时内接于圆,则圆心O是这两个三角形的( )
| A、重心 | B、垂心 |
| C、外心 | D、重心和垂心 |
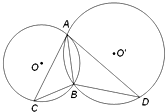 如图,⊙O和⊙O′相交于A、B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB、CB,已知BC=3,BD=4,则AB=
如图,⊙O和⊙O′相交于A、B两点,过A作两圆的切线分别交两圆于C、D两点,连接DB、CB,已知BC=3,BD=4,则AB=