题目内容
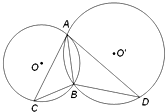如图，⊙O和⊙O′相交于A、B两点，过A作两圆的切线分别交两圆于C、D两点，连接DB、CB，已知BC=3，BD=4，则AB=考点：与圆有关的比例线段
专题：计算题,立体几何
分析：先由AC与⊙O′相切于A，得∠CAB=∠ADB，同理得到∠ACB=∠DAB，即可得到△ACB∽△DAB，进而得到结论．
解答：
解：由AC与⊙O′相切于A，
得∠CAB=∠ADB，
同理∠ACB=∠DAB，
所以△ACB∽△DAB，
从而
=
，
即AB2=BC•BD．
因为BC=3，BD=4，
所以AB=2
．
故答案为：2
．
得∠CAB=∠ADB，
同理∠ACB=∠DAB，
所以△ACB∽△DAB，
从而
| CB |
| AB |
| AB |
| DB |
即AB2=BC•BD．
因为BC=3，BD=4，
所以AB=2
| 3 |
故答案为：2
| 3 |
点评：本题主要考查与圆有关的比例线段、相似三角形的判定及切线性质的应用．属于基础题．
练习册系列答案
相关题目
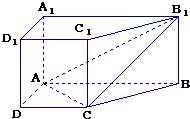直棱柱ABCD-A1B1C1D1中，底面ABCD是直角梯形，∠BAD=∠ADC=90°，AB=2AD=2CD=2．
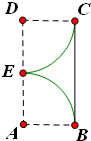如图，在矩形ABCD中，E为边AD的中点，AB=1，BC=2，分别以A，D为圆心，1为半径作圆弧EB，EC，若由两圆弧EB，EC及边BC所围成的平面图形绕直线AD旋转一周，则所形成的几何体的表面积为如果复数z满足（2+i）z=5i（i是虚数单位），则z（ ）
| A、1+2i | B、-1+2i |
| C、2+i | D、1-2i |