题目内容
数列{an}的前n项的和Sn=2n-1,则an= .
考点:数列递推式
专题:等差数列与等比数列
分析:利用公式an=
求解.
|
解答:
解:∵数列{an}的前n项的和Sn=2n-1,
∴n=1时,a1=S1=2-1=1;
n≥2时,an=Sn-Sn-1
=(2n-1)-(2n-1-1)
=2n-1.
n=1时,2n-1=1=a1.
∴an=2n-1.
故答案为:2n-1.
∴n=1时,a1=S1=2-1=1;
n≥2时,an=Sn-Sn-1
=(2n-1)-(2n-1-1)
=2n-1.
n=1时,2n-1=1=a1.
∴an=2n-1.
故答案为:2n-1.
点评:本题考查数列的通项公式的求法,解题时要认真审题,是基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
由函数y=x2的图象与直线x=1、x=2和x轴所围成的封闭图形的面积是( )
| A、3 | ||
B、
| ||
| C、2 | ||
D、
|
要得到函数y=2sin2x的图象,只需要将函数y=2sin(2x-
)的图象( )
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
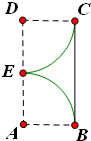 如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A,D为圆心,1为半径作圆弧EB,EC,若由两圆弧EB,EC及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的表面积为
如图,在矩形ABCD中,E为边AD的中点,AB=1,BC=2,分别以A,D为圆心,1为半径作圆弧EB,EC,若由两圆弧EB,EC及边BC所围成的平面图形绕直线AD旋转一周,则所形成的几何体的表面积为