题目内容
已知
=（2，3），
=（-1，2）当k为何值时，
（Ⅰ）k
+
与
-3
垂直？
（Ⅱ）k
+
与
-3
平行？平行时它们是同向还是反向？
| a |
| b |
（Ⅰ）k
| a |
| b |
| a |
| b |
（Ⅱ）k
| a |
| b |
| a |
| b |
考点：平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：先求出k
+
与
-3
的坐标，
（1）利用向量垂直的充要条件：数量积为0，列出方程求出k．
（2）利用向量共线的坐标形式的充要条件：坐标交叉相乘相等，列出方程求出k，将k代入两向量的坐标，判断出方向相反．
| a |
| b |
| a |
| b |
（1）利用向量垂直的充要条件：数量积为0，列出方程求出k．
（2）利用向量共线的坐标形式的充要条件：坐标交叉相乘相等，列出方程求出k，将k代入两向量的坐标，判断出方向相反．
解答：
解：k
+
=k（2，3）+（-1，2）=（2k-1，3k+2），
-3
=（5，-3）
（1）k
+
与
-3
垂直，得（k
+
）•（
-3
）=10k-5-9k-6=k-11=0，k=11
（2）k
+
与
-3
平行，
得15k+10=-6k+3，k=-
此时kk
+
=（-
，1），
-3
=（5，-3），所以方向相反．
| a |
| b |
| a |
| b |
（1）k
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（2）k
| a |
| b |
| a |
| b |
得15k+10=-6k+3，k=-
| 1 |
| 3 |
此时kk
| a |
| b |
| 5 |
| 3 |
| a |
| b |
点评：本题考查向量的坐标运算、向量垂直的充要条件、向量的坐标形式的数量积公式、向量共线的坐标形式的充要条件．
练习册系列答案
相关题目
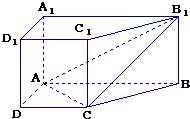直棱柱ABCD-A1B1C1D1中，底面ABCD是直角梯形，∠BAD=∠ADC=90°，AB=2AD=2CD=2．
如图，在四棱锥S-ABCD中，平面SAD⊥平面ABCD，四边形ABCD为正方形，且P为AD的中点，Q为SB的中点，M为BC的中点．