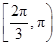题目内容
在边长为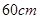 的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
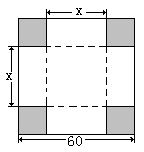
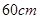 的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
的正方形铁皮的四切去相等的正方形,再把它的边沿虚线折起,做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
当箱底边长为 时,箱子容积最大,最大容积是
时,箱子容积最大,最大容积是 .
.
 时,箱子容积最大,最大容积是
时,箱子容积最大,最大容积是 .
.试题分析:设箱底边长为

 ,则无盖的方底箱子的高
,则无盖的方底箱子的高
 ,其体积为
,其体积为 ,从而可得
,从而可得 ,通过求导,讨论导数的正负得函数的增减性,根据函数的单调性可求体积的最大值.
,通过求导,讨论导数的正负得函数的增减性,根据函数的单调性可求体积的最大值.试题解析:设箱底边长为

 ,则无盖的方底箱子的高
,则无盖的方底箱子的高
 ,其体积为
,其体积为
则


令
 ,得
,得 ,解得
,解得 (
( 舍去)
舍去) 当
 时,
时, ;当
;当 时,
时,
所以
 时,
时, 单调递增;
单调递增; 时,
时, 单调递减,所以函数
单调递减,所以函数 在
在 时取得极大值, 结合实际情况,这个极大值就是函数
时取得极大值, 结合实际情况,这个极大值就是函数 的最大值.
的最大值. 
故当箱底边长为
 时,箱子容积最大,最大容积是
时,箱子容积最大,最大容积是 .
. 
练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
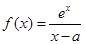 ,(其中常数
,(其中常数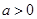 )
)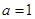 时,求曲线在
时,求曲线在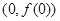 处的切线方程;
处的切线方程;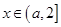 使得不等式
使得不等式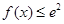 成立,求
成立,求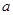 的取值范围.
的取值范围.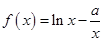 ,其中
,其中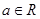 .
.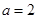 时,求函数
时,求函数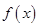 的图象在点
的图象在点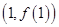 处的切线方程;
处的切线方程;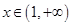 ,都有
,都有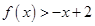 ,求
,求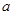 的取值范围.
的取值范围.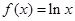 ,
,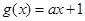 ,
,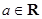 ,记
,记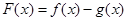 .
.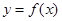 在
在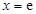 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; 时,若函数
时,若函数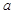 的取值范围.
的取值范围.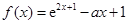 ,
,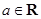 .
.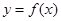 在点
在点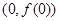 处的切线与直线
处的切线与直线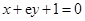 垂直,求
垂直,求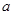 的值;
的值; 的单调区间;
的单调区间;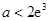 ,当
,当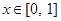 时,都有
时,都有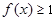 成立,求实数
成立,求实数 在曲线
在曲线 上,
上, 为曲线在点
为曲线在点



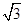 ),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )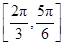
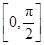 ∪
∪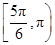
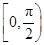 ∪
∪