题目内容
16.设a∈R,函数f(x)=e-x(a+ex-x2)(1)若a=1,求曲线y=f(x)在点(-1,f(-1))处的切线方程;
(2)判断f(x)在R上的单调性.
分析 (1)先求出f′(x),把a=1代入f′(x)确定其解析式,根据曲线y=f(x)的切点(-1,f(-1))得到切线的斜率k=f′(-1),把x=-1代入f(x)中求出f(-1)得到切点的坐标,利用切点坐标和斜率写出切线方程即可;
(2)令f′(x)=0即可得到函数的单调区间.
解答 解:∵f(x)=e-x(a+ax-x2)
∴f′(x)=-e-x(a+ex-x2)+e-x(e-2x)=e-x[x2-(e+2)x+e-a],
(1)当a=1时f′(x)=e-x[x2-(e+2)x+e-1],
则f′(-1)=2e2+2e,f(-1)=e(1-1-12)=-e2,
所以切点坐标为(-1,-e2),切线斜率k=2e2+2e
则切线方程为y=(2e2+2e)x+e2+2e;
(2)令g(x)=x2-(e+2)x+e-a,
△=(e+2)2-4(e-a)≤0即a≤-$\frac{{e}^{2}}{4}$-1时,
g(x)≥0,又∵e-x>0,∴f′(x)≥0,
此时f(x)在R上单调递增;
当△>0即a>-$\frac{{e}^{2}}{4}$-1时,
令f′(x)=0,即g(x)=0,x=$\frac{e+2±\sqrt{{e}^{2}+4a+4}}{2}$,
令f′(x)>0,解得:x>$\frac{e+2+\sqrt{{e}^{2}+4a+4}}{2}$或x<$\frac{e+2-\sqrt{{e}^{2}+4a+4}}{2}$,
令f′(x)<0,解得:$\frac{e+2-\sqrt{{e}^{2}+4a+4}}{2}$<x<$\frac{e+2+\sqrt{{e}^{2}+4a+4}}{2}$,
∴f(x)在($\frac{e+2+\sqrt{{e}^{2}+4a+4}}{2}$,+∞),(-∞,$\frac{e+2-\sqrt{{e}^{2}+4a+4}}{2}$)递增,
在($\frac{e+2-\sqrt{{e}^{2}+4a+4}}{2}$,$\frac{e+2+\sqrt{{e}^{2}+4a+4}}{2}$)递减.
点评 此题是一道综合题,要求学生会根据导数求曲线上某点切线的斜率以及会根据一点和斜率写出切线的方程,会利用导数研究函数的单调性.

| A. | 命题“p∧q”是真命题 | B. | 命题“p∧(¬q)”是真命题 | ||
| C. | 命题“(¬p)∧q”为真命题 | D. | 命题“(¬p)∧(¬q)”是真命题 |
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{3}{2}$i | D. | -$\frac{3}{2}$i |
| A. | 3 | B. | 6 | C. | $6\sqrt{2}$ | D. | 2 |
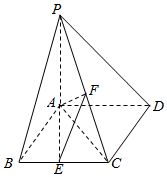 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.