题目内容
10.已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),P为椭圆上与长轴端点不重合的一点,F1,F2分别为椭圆的左、右焦点,过F2作∠F1PF2外角平分线的垂线,垂足为Q,若|OQ|=2b,椭圆的离心率为e,则$\frac{{a}^{2}+{e}^{2}}{2b}$的最小值为$\sqrt{3}$.分析 由题意画出图形,利用转化思想方法求得OQ=a,又OQ=2b,得a=2b,进一步得到a,e与b的关系,然后利用基本不等式求得$\frac{{a}^{2}+{e}^{2}}{2b}$的最小值.
解答 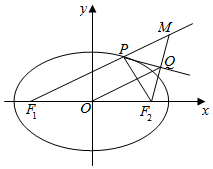 解:如图,
解:如图,
由题意,P是以F1,F2为焦点的椭圆上一点,过焦点F2作∠F1PF2外角平分线的垂线,垂足为Q,延长F2Q交F1P延长线于M,得PM=PF2,
由椭圆的定义知PF1+PF2=2a,故有PF1+PM=MF1=2a,
连接OQ,知OQ是三角形F1F2M的中位线,
∴OQ=a,又OQ=2b,
∴a=2b,则a2=4b2=4(a2-c2),即${c}^{2}=\frac{3}{4}{a}^{2}$,
∴$\frac{{a}^{2}+{e}^{2}}{2b}$=$\frac{{a}^{2}+\frac{{c}^{2}}{{a}^{2}}}{2b}$=$\frac{{a}^{4}+{c}^{2}}{2{a}^{2}b}=\frac{16{b}^{4}+\frac{3}{4}•4{b}^{2}}{8{b}^{3}}$=$2b+\frac{3}{8b}≥2\sqrt{2b•\frac{3}{8b}}=\sqrt{3}$.
当且仅当$2b=\frac{3}{8b}$,即${b}^{2}=\frac{3}{16}$,即$b=\frac{\sqrt{3}}{4}$时,$\frac{{a}^{2}+{e}^{2}}{2b}$有最小值为$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查椭圆的简单性质,考查了数学转化思想方法,训练了利用基本不等式求最值,是中档题.

练习册系列答案
相关题目
20.若函数f(x)=(k2+1)lnx-x2在区间(1,+∞)上是减函数,则实数k的取值范围是( )
| A. | [-1,1] | B. | [-$\sqrt{2}$,$\sqrt{2}$] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-$\sqrt{2}$]∪[$\sqrt{2}$,+∞) |
5.焦点在x轴上的椭圆$\frac{x^2}{3n}+{y^2}=1(n>0)$的焦距为$4\sqrt{2}$,则长轴长是( )
| A. | 3 | B. | 6 | C. | $6\sqrt{2}$ | D. | 2 |
16.设α为锐角,则“log2tanα>1”是“0<sin2α<$\frac{4}{5}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 正四棱柱ABCD-A1B1C1D1底面边长为$\sqrt{3}$,高为1,O为下底面的中心.
正四棱柱ABCD-A1B1C1D1底面边长为$\sqrt{3}$,高为1,O为下底面的中心.