题目内容
11.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(0)=( )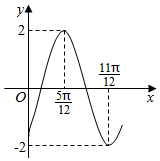
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -1 | D. | -$\frac{1}{2}$ |
分析 根据函数在同一周期内的最大值、最小值对应的x值,求出函数的周期T=$\frac{2π}{ω}$=π,解得ω=2.由函数当x=$\frac{5π}{12}$时取得最大值2,得到$\frac{5π}{6}$+φ=$\frac{π}{2}$+kπ(k∈Z),取k=0得到φ=-$\frac{π}{3}$.求得函数解析式,代入即可得到本题的答案.
解答 解:∵在同一周期内,函数在x=$\frac{5π}{12}$时取得最大值,x=$\frac{11π}{12}$时取得最小值,
∴函数的周期T满足$\frac{T}{2}$=$\frac{11π}{12}$-$\frac{5π}{12}$=$\frac{π}{2}$,
由此可得T=$\frac{2π}{ω}$=π,解得ω=2,
得函数表达式为f(x)=2sin(2x+φ),
又∵当x=$\frac{5π}{12}$时取得最大值2,
∴2sin(2•$\frac{5π}{12}$+φ)=2,可得$\frac{5π}{6}$+φ=$\frac{π}{2}$+2kπ(k∈Z),
∵-$\frac{π}{2}$<φ<$\frac{π}{2}$,∴取k=0,得φ=-$\frac{π}{3}$.
∴可得f(x)=2sin(2x-$\frac{π}{3}$),f(0)=2sin(-$\frac{π}{3}$)=-$\sqrt{3}$.
故选:A.
点评 本题给出y=Asin(ωx+φ)的部分图象,求函数的表达式.着重考查了三角函数的图象与性质、函数y=Asin(ωx+φ)的图象变换等知识,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.焦点在x轴上的椭圆$\frac{x^2}{3n}+{y^2}=1(n>0)$的焦距为$4\sqrt{2}$,则长轴长是( )
| A. | 3 | B. | 6 | C. | $6\sqrt{2}$ | D. | 2 |
3.在△ABC中,若c=2,b=2a,且cosC=$\frac{1}{4}$,则a等于( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{1}{3}$ |
16.设α为锐角,则“log2tanα>1”是“0<sin2α<$\frac{4}{5}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.在一次考试中,5名同学的数学、物理成绩如表所示:
(1)根据表中数据,求物理分y关于数学分x的回归方程;
(2)试估计某同学数学考100分时,他的物理得分;
(3)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以X表示选中的同学中物理成绩高于90分的人数,试解决下列问题:
①求至少选中1名物理成绩在90分以下的同学的概率;
②求随机变变量X的分布列及数学期望E(X).
(附:回归方程::$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$)
| 学生 | A | B | C | D | E |
| 数学(x分) | 89 | 91 | 93 | 95 | 97 |
| 物理(y分) | 87 | 89 | 89 | 92 | 93 |
(2)试估计某同学数学考100分时,他的物理得分;
(3)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以X表示选中的同学中物理成绩高于90分的人数,试解决下列问题:
①求至少选中1名物理成绩在90分以下的同学的概率;
②求随机变变量X的分布列及数学期望E(X).
(附:回归方程::$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$)