题目内容

15．已知复数Z的共轭复数$\overline{Z}$=$\frac{1-i}{1+2i}$，则复数Z的虚部是（　　）
A．$\frac{3}{5}$B．$\frac{3}{5}$iC．-$\frac{3}{5}$D．-$\frac{3}{5}$i

分析 利用复数代数形式的乘除运算化简，求得Z后得答案．

解答 解：由$\overline{Z}$=$\frac{1-i}{1+2i}$=$\frac{（1-i）（1-2i）}{（1+2i）（1-2i）}=\frac{-1-3i}{5}=-\frac{1}{5}-\frac{3}{5}i$，
得$Z=-\frac{1}{5}+\frac{3}{5}i$，
∴复数Z的虚部是$\frac{3}{5}$．
故选：A．

点评 题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

练习册系列答案
相关题目
18．在△ABC中，∠B=90°，AB=3，BC=4，O为△ABC内心，则$\overrightarrow{AO}•\overrightarrow{BC}$=4．
6．已知命题：p?x∈（0，$\frac{π}{2}$），sinx+cosx＞1恒成立，命题q：?x∈（0，$\frac{π}{2}$），使2x＞3x，则下列结论中正确的是（　　）
A．命题“p∧q”是真命题B．命题“p∧（￢q）”是真命题
C．命题“（￢p）∧q”为真命题D．命题“（￢p）∧（￢q）”是真命题
3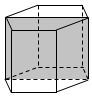．如图，已知正六棱柱的最大对角面的面积为1m2，互相平行的两个侧面的距离为1m，则这个六棱柱的体积为（　　）
A．$\frac{{3\sqrt{3}}}{4}$m3B．$\frac{3}{4}$m3C．1m3D．$\frac{1}{2}$m3
10．不等式组$\left\{\begin{array}{l}x≥0\\ x+3y≥4\\ 3x+y≤4\end{array}\right.$所表示的平面区域的面积为$\frac{4}{3}$，若lgy-lg（x+a）的最大值是1，则正数a的值是$\frac{2}{5}$．
20．若函数f（x）=（k2+1）lnx-x2在区间（1，+∞）上是减函数，则实数k的取值范围是（　　）
A．[-1，1]B．[-$\sqrt{2}$，$\sqrt{2}$]C．（-∞，-1]∪[1，+∞）D．（-∞，-$\sqrt{2}$]∪[$\sqrt{2}$，+∞）
7．已知双曲线的中心在坐标原点，焦点在坐标轴上，双曲线上一点M与两焦点的距离的差的绝对值等于6，且离心率e=$\frac{5}{3}$，则该双曲线的焦距长为10．
4．在△ABC中，角A，B，C的对边分别为a，b，c，且满足（2a-b）cosC-ccosB=0．
（Ⅰ）求角C的值；
（Ⅱ）若三边a，b，c满足a+b=13，c=7，求△ABC的面积．
5．焦点在x轴上的椭圆$\frac{x^2}{3n}+{y^2}=1（n＞0）$的焦距为$4\sqrt{2}$，则长轴长是（　　）
A．3B．6C．$6\sqrt{2}$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网