题目内容
设随机变量 ξ~N(μ,σ2),且 P(ξ<-1)=P(ξ>1),P(ξ>2)=0.3,则P(-2<ξ<0)= .
考点:正态分布曲线的特点及曲线所表示的意义
专题:计算题,概率与统计
分析:根据正态分布的性质求解.
解答:
解:因为P(ξ<-1)=P(ξ>1),所以正态分布曲线关于y轴对称,
又因为P(ξ>2)=0.3,所以P(-2<ξ<0)=
=0.2
故答案为:0.2.
又因为P(ξ>2)=0.3,所以P(-2<ξ<0)=
| 1-2×0.3 |
| 2 |
故答案为:0.2.
点评:一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似的服从正态分布,正态分布在概率和统计中具有重要地位.

练习册系列答案
相关题目
不等式
<0成立的一个充分不必要条件是( )
| 1-x |
| x |
| A、x>1 | B、x<0或x>1 |
| C、0<x<1 | D、x≤0 |
将函数y=3sin(2x-
)的图象经过( )变换,可以得到函数y=3sin2x的图象.
| π |
| 4 |
A、沿x轴向右平移
| ||
B、沿x轴向左平移
| ||
C、沿x轴向右平移
| ||
D、沿x轴向左平移
|
已知函数f(x)=2
cosxsin(x+
)-1(x∈R).则函数f(x)在区间[-
,
]上的最大值和最小值分别是( )
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
A、最大值为
| ||||
B、最大值为
| ||||
C、最大值为2
| ||||
| D、最大值为1,最小值为-1 |
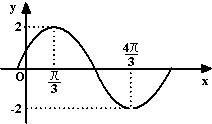 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<