题目内容
已知cosα=
,α∈(0,π),则cos(α-
)的值为( )
| 3 |
| 5 |
| π |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:利用同角的三角函数基本关系式和两角和差的余弦公式即可得出.
解答:
解:∵cosα=
,α∈(0,π),
∴sinα=
=
.
∴cos(α-
)=cosαcos
+sinαsin
=
×
+
×
=
.
故选:C.
| 3 |
| 5 |
∴sinα=
| 1-cos2α |
| 4 |
| 5 |
∴cos(α-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
4+3
| ||
| 10 |
故选:C.
点评:本题考查了同角的三角函数基本关系式和两角和差的余弦公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若输入a=3,b=4,则通过如图程序框图输出结果是( )


| A、±5 | B、-5 | C、5 | D、4 |
圆(x+2)2+(y+1)2=4关于x轴对称的圆的方程为( )
| A、(x-2)2+(y+1)2=4 |
| B、(x+2)2+(y-1)2=4 |
| C、(x-2)2+(y-1)2=4 |
| D、(x+2)2+(y+1)2=4 |
在平面直角坐标系中,直线x-y=0与曲线y=x2-2x所围成的面积为( )
| A、1 | ||
B、
| ||
C、
| ||
| D、9 |
1426和1643的最大公约数是( )
| A、34 | B、12 | C、93 | D、31 |
函数f(x)=cos2x+
sinxcosx在区间[-
,
]上的最大值为( )
| 3 |
| π |
| 4 |
| π |
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
已知f(x)=
,则
的值是( )
| 1 |
| x |
| lim |
| △x→0 |
| -f(2+△x)+f(2) |
| △x |
A、
| ||
| B、2 | ||
C、-
| ||
| D、-2 |
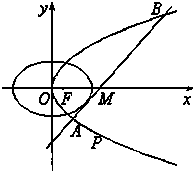 已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.
已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.