题目内容
13.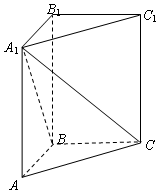 在正三棱柱ABC-A1B1C1中,AB=1,BB1=2,求:
在正三棱柱ABC-A1B1C1中,AB=1,BB1=2,求:(1)异面直线B1C1与A1C所成角的大小;
(2)四棱锥A1-B1BCC1的体积.
分析 (1)由B1C1∥BC,知∠BCA1是异面直线B1C1与A1C所成角,由此能求出异面直线B1C1与A1C所成角大小.
(2)四棱锥A1-B1BCC1的体积V=${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}-{V}_{{A}_{1}-ABC}$,由此能求出结果.
解答 解:(1)∵正三棱柱ABC-A1B1C1,∴B1C1∥BC,
∴∠BCA1是异面直线B1C1与A1C所成角,…(2分)
在△BCA1中,BC=1,${A}_{1}B=\sqrt{5}$,${A}_{1}C=\sqrt{5}$,
∴cos∠BCA1=$\frac{B{C}^{2}+C{{A}_{1}}^{2}-B{{A}_{1}}^{2}}{2BC•C{A}_{1}}$=$\frac{\sqrt{5}}{10}$,…(5分)
∴$∠BC{A_1}=arccos\frac{{\sqrt{5}}}{10}$,
∴异面直线B1C1与A1C所成角大小为arccos$\frac{\sqrt{5}}{10}$.…(7分)
(2)∵正三棱柱ABC-A1B1C1中,AB=1,BB1=2,
∴${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$=S△ABC•AA1=$\frac{\sqrt{3}}{2}$,
${V}_{{A}_{1}-ABC}=\frac{1}{3}{S}_{△ABC}•A{A}_{1}=\frac{\sqrt{3}}{6}$,
∴四棱锥A1-B1BCC1的体积V=${V}_{ABC-{A}_{1}{B}_{1}{C}_{1}}-{V}_{{A}_{1}-ABC}$=$\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{6}=\frac{\sqrt{3}}{3}$.…(14分)
点评 本题考查异面直线所成角的大小的求法,考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

| A. | 若m∥α,m、n不平行,则n与α不平行 | B. | 若m∥α,m、n不垂直,则n与α不垂直 | ||
| C. | 若m⊥α,m、n不平行,则n与α不垂直 | D. | 若m⊥α,m、n不垂直,则n与α不平行 |
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | (0,1) | D. | $({0,\frac{1}{2}})∪$$({\frac{1}{2},1})$ |
| A. | x=0或x=log25 | B. | x=-1或x=5 | C. | x=log25 | D. | x=0 |