题目内容
2．在无穷等比数列{an}中，$\lim_{n→∞}（{a_1}+{a_2}+…+{a_n}）=\frac{1}{2}$，则a1的取值范围是（ ）| A． | $（{0，\frac{1}{2}}）$ | B． | $（{\frac{1}{2}，1}）$ | C． | （0，1） | D． | $（{0，\frac{1}{2}}）∪$$（{\frac{1}{2}，1}）$ |
分析 利用无穷等比数列和的极限，列出方程，推出a1的取值范围．
解答 解：在无穷等比数列{an}中，$\lim_{n→∞}（{a_1}+{a_2}+…+{a_n}）=\frac{1}{2}$，
可知|q|＜1，则$\frac{{a}_{1}}{1-q}$=$\frac{1}{2}$，
a1=$\frac{1}{2}（1-q）$∈（0，$\frac{1}{2}$）∪（$\frac{1}{2}$，1）．
故选：D．
点评 本题考查数列的极限的求法，等比数列的应用，考查计算能力．
练习册系列答案
相关题目
12．甲乙两人有三个不同的学习小组A，B，C可以参加，若每人必须参加并且仅能参加一个学习小组，则两人参加不同小组的概率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{6}$ | D． | $\frac{5}{6}$ |
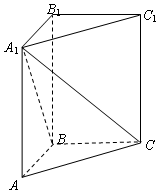在正三棱柱ABC-A1B1C1中，AB=1，BB1=2，求：
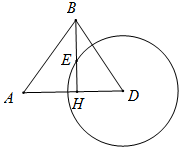如图，我海监船在D岛海域例行维权巡航，某时刻航行至A处，此时测得其北偏东30°方向与它相距20海里的B处有一外国船只，且D岛位于海监船正东18海里处．