题目内容
已知双曲线C的中心在原点,且左、右焦点分别为F1,F2,以F1F2为底边作正三角形,若双曲线C与该正三角形两腰的交点恰为两腰的中点,则双曲线C的离心率为 .
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设以F1F2为底边的正三角形与双曲线C的右支交于点M,则在Rt△MF1F2中可得|F1F2|=2c,|MF1|=
c,|MF2|=c,由双曲线定义列出a,c 的关系式,求出离心率.
| 3 |
解答:
解:依题意知,设以F1F2为底边的正三角形与双曲线C的右支交于点M,
则在Rt△MF1F2中可得|F1F2|=2c,|MF1|=
c,|MF2|=c,
由双曲线的定义有|MF1|-|MF2|=2a即
c-c=2a,
所以双曲线C的离心率e=
=
=
+1.
故答案为:
+1.
则在Rt△MF1F2中可得|F1F2|=2c,|MF1|=
| 3 |
由双曲线的定义有|MF1|-|MF2|=2a即
| 3 |
所以双曲线C的离心率e=
| c |
| a |
| 2 | ||
|
| 3 |
故答案为:
| 3 |
点评:本题考查双曲线的定义、考查离心率的求法:找a,b,c的关系式,属于一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设f(x)=x-aex(a∈R),x∈R,已知函数y=f(x)有两个零点x1,x2,且x1<x2.
(Ⅰ)求a的取值范围;
(Ⅱ)证明:
随着a的减小而增大;
(Ⅲ)证明x1+x2随着a的减小而增大.
(Ⅰ)求a的取值范围;
(Ⅱ)证明:
| x2 |
| x1 |
(Ⅲ)证明x1+x2随着a的减小而增大.
若sina=
,a是第二象限的角,则cosa=( )
| 4 |
| 5 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
设a,b∈R,则“a3<b3”是“a<b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若三个互不相等的正数x1,x2,x3满足方程xi+lnxi=mi(i=1,2,3),且m1+m3=2m2,则下列关系式正确的是( )
| A、x1x3<x22 |
| B、x1x3≤x22 |
| C、x1x3>x22 |
| D、x1x3≥x22 |
设x,y满足约束条件
,则
的取值范围是( )
|
| x+2y+3 |
| x+1 |
| A、[3,11] |
| B、[3,10] |
| C、[2,6] |
| D、[1,5] |
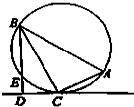 如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为
如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为