题目内容
在直角坐标系xOy中,曲线C1的参数方程为
(t为参数),P为C1上的动点,Q为线段OP的中点.
①求点Q的轨迹C2的方程;
②在以O为极点,x轴的正半轴为极轴(两坐标系取相同的长度单位)的极坐标系中,N为曲线p=2sinθ上的动点,M为C2与x轴的交点,求|MN|的最大值.
|
①求点Q的轨迹C2的方程;
②在以O为极点,x轴的正半轴为极轴(两坐标系取相同的长度单位)的极坐标系中,N为曲线p=2sinθ上的动点,M为C2与x轴的交点,求|MN|的最大值.
考点:点的极坐标和直角坐标的互化,参数方程化成普通方程
专题:坐标系和参数方程
分析:①设点Q的坐标为(x,y),则由题意可得P(2x,2y),且
,由此可得点Q的轨迹C2的方程.
②由题意可得,点M(1,0),曲线p=2sinθ化为直角坐标方程,表示以A(0,1)为圆心、半径为1的圆.
则|MN|的最大值即为|AM|+1.
|
②由题意可得,点M(1,0),曲线p=2sinθ化为直角坐标方程,表示以A(0,1)为圆心、半径为1的圆.
则|MN|的最大值即为|AM|+1.
解答:
解:①设点Q的坐标为(x,y),则由题意可得P(2x,2y),∴
,
即
(t为参数).
②由题意可得,点M(1,0),曲线p=2sinθ的直角坐标方程为 x2+(y-1)2=1,
表示以A(0,1)为圆心、半径为1的圆.
由于|AM|=
,∴|MN|的最大值为1+
.
|
即
|
②由题意可得,点M(1,0),曲线p=2sinθ的直角坐标方程为 x2+(y-1)2=1,
表示以A(0,1)为圆心、半径为1的圆.
由于|AM|=
| 2 |
| 2 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,求点的轨迹方程,直线和圆的位置关系,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
设f(x)=x-aex(a∈R),x∈R,已知函数y=f(x)有两个零点x1,x2,且x1<x2.
(Ⅰ)求a的取值范围;
(Ⅱ)证明:
随着a的减小而增大;
(Ⅲ)证明x1+x2随着a的减小而增大.
(Ⅰ)求a的取值范围;
(Ⅱ)证明:
| x2 |
| x1 |
(Ⅲ)证明x1+x2随着a的减小而增大.
若三个互不相等的正数x1,x2,x3满足方程xi+lnxi=mi(i=1,2,3),且m1+m3=2m2,则下列关系式正确的是( )
| A、x1x3<x22 |
| B、x1x3≤x22 |
| C、x1x3>x22 |
| D、x1x3≥x22 |
 已知斜三棱柱的三视图如图所示,该斜三棱柱的体积为
已知斜三棱柱的三视图如图所示,该斜三棱柱的体积为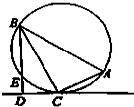 如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为
如图,在△ABC中,∠C=90°,∠A=60°,过C作△ABC的外接圆的切线CD,BD⊥CD于D.BD与外接圆交于点E,已知DE=5,则△ABC的外接圆的半径为