题目内容
已知曲线C:
(θ为参数),直线l的极坐标方程为ρsinθ+3=0(以直角坐标原点O为极点,x轴非负半轴为极轴建立极坐标系),则C被l截得弦长为 .
|
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:把曲线C的参数方程化为普通方程,直线l的极坐标方程化为普通方程,两方程联立,求得弦长|AB|的端点坐标,即得|AB|的大小.
解答:
解:把曲线C的参数方程化为普通方程,得
(x-2)2+(y+2)2=4…①;
把直线l的极坐标方程化为普通方程,得
y+3=0…②;
由①、②解得x1=2+
,x2=2-
,
∴弦长|AB|=|x1-x2|=|(2+
)-(2-
)|=2
.
故答案为:2
.
(x-2)2+(y+2)2=4…①;
把直线l的极坐标方程化为普通方程,得
y+3=0…②;
由①、②解得x1=2+
| 3 |
| 3 |
∴弦长|AB|=|x1-x2|=|(2+
| 3 |
| 3 |
| 3 |
故答案为:2
| 3 |
点评:本题考查了参数方程与极坐标的应用问题,解题时应先把参数方程与极坐标化为普通方程,再来解答,是基础题.

练习册系列答案
相关题目
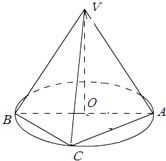 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,已知AB=2,VA=VB=VC=2.

 一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积V=
一个四棱锥的三视图如图所示,其左视图是等边三角形,该四棱锥的体积V=