题目内容
已知l1、l2是曲线C:y=
的两条互相平行的切线,则l1与l2与的距离的最大值为 .
| 1 |
| x |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:首先设出两切点,求出导数,求出斜率,写出两切线方程,运用两平行直线的距离公式化简整理,再运用基本不等式即可求出最大值,注意等号成立的条件.
解答:
解:设l1,l2与曲线相切的切点分别是P1(x1,y1),P2(x2,y2),
则y1=
,y2=
,
又y′=(
)′=-
,
∵l1∥l2,∴-
=-
,∴x2=-x1,
∴l1:y-y1=-
(x-x1)即y=-
x+
,
l2:y-y2=-
(x-x2)即y=-
x-
,
∴由两平行线的距离公式得,d=
=
≤
=2
.当且仅当x12=
即x1=±1时,d取得最大值2
.
故答案为:2
.
则y1=
| 1 |
| x1 |
| 1 |
| x2 |
又y′=(
| 1 |
| x |
| 1 |
| x2 |
∵l1∥l2,∴-
| 1 |
| x12 |
| 1 |
| x22 |
∴l1:y-y1=-
| 1 |
| x12 |
| 1 |
| x12 |
| 2 |
| x1 |
l2:y-y2=-
| 1 |
| x22 |
| 1 |
| x12 |
| 2 |
| x1 |
∴由两平行线的距离公式得,d=
| ||||
|
| 4 | ||||
|
| 4 | ||
|
| 2 |
| 1 |
| x12 |
| 2 |
故答案为:2
| 2 |
点评:本题考查导数的概念及应用,应用导数的几何意义是求切线方程的关键,同时考查两平行直线的距离公式及基本不等式的运用,熟记这些公式是迅速解题的前提.

练习册系列答案
相关题目
若角α的终边经过点P(1,-2),则sinα=( )
A、
| ||||
B、-
| ||||
| C、-2 | ||||
D、-
|
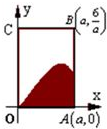 如图,矩形OABC内阴影部分是由曲线f(x)=sinx(x∈(0,π)及直线x=a(a∈(0,π)与x轴围成,向矩形OABC内随机的投掷一点,若落在阴影部分的概率为
如图,矩形OABC内阴影部分是由曲线f(x)=sinx(x∈(0,π)及直线x=a(a∈(0,π)与x轴围成,向矩形OABC内随机的投掷一点,若落在阴影部分的概率为 从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图所示,则直方图中x的值为
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图所示,则直方图中x的值为