题目内容
已知向量
=(x,-2),
=(1,-x),其中x∈R,若
∥
,则实数x的值为 .
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用向量共线定理即可得出.
解答:
解:∵
∥
,
∴-2+x2=0,
解得x=±
.
故答案为:±
.
| a |
| b |
∴-2+x2=0,
解得x=±
| 2 |
故答案为:±
| 2 |
点评:本题考查了向量共线定理,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,点G为△ABC的重心.已知|AB|=2
,且向量
与
的夹角为120°,则
•
的最小值是
( )
| 3 |
| GA |
| GB |
| CA |
| CB |
( )
| A、-3 | B、6 | C、9 | D、24 |
在数列{an}中,已知an=
(c∈R),则对于任意正整数n有( )
| n+c |
| n+1 |
| A、an<an+1 |
| B、an与an+1的大小关系和c有关 |
| C、an>an+1 |
| D、an与an+1的大小关系和n有关 |
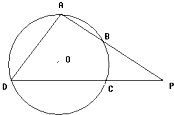 (选修4-1:几何证明选讲)如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.若AB=BC=2,则CD=
(选修4-1:几何证明选讲)如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.若AB=BC=2,则CD=