题目内容
已知函数f(x)=x|x-a|(a∈R)
(1)若a=2,解关于x的不等式f(x)<x;
(2)若对任意的x∈(0,4]都有f(x)<4,求a的取值范围.
(1)若a=2,解关于x的不等式f(x)<x;
(2)若对任意的x∈(0,4]都有f(x)<4,求a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)当a=2时,不等式f(x)<x即x|x-2|<x,再分x>0、x<0两种情况,分别求得x的范围,可得不等式f(x)<x的解集.
(Ⅱ)由题意可得对任意的x∈(0,4],都有f(x)<4,即x-
<a<x+
恒成立.设g(x)=x-
,p(x)=x+
,利用导数求的g(x)的最大值和p(x)的最小值,可得a的范围.
(Ⅱ)由题意可得对任意的x∈(0,4],都有f(x)<4,即x-
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
解答:
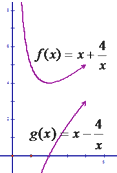 解:(Ⅰ)当a=2时,不等式f(x)<x即x|x-2|<x,
解:(Ⅰ)当a=2时,不等式f(x)<x即x|x-2|<x,
显然x≠0,当x>0时,原不等式可化为:|x-2|<1,即-1<x-2<1,
解得 1<x<3.
当x<0时,原不等式可化为:|x-2|>1,即x-2>1 或x-2<-1,求得x<0.
综上得:当a=2时,原不等式的解集为{x|1<x<3 或x<0}.
(Ⅱ)∵对任意的x∈(0,4]都有f(x)<4,即-4<x(x-a)<4,
对任意的x∈(0,4]都有x-
<a<x+
恒成立.
设g(x)=x-
,p(x)=x+
,x∈(0,4],如图所示:
问题等价于x∈(0,4]时,g(x)max<a<p(x)min.
∵g′(x)=1+
>0,∴函数g(x)在(0,4]上单调递增,g(x)max=g(4)=3.
又∵p′(x)=1-
=
,∴p(x)在(0,2]上递减,在[2,4]上递增,
∴p(x)min=p(2)=4 a∈(3,4).
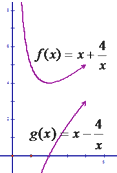 解:(Ⅰ)当a=2时,不等式f(x)<x即x|x-2|<x,
解:(Ⅰ)当a=2时,不等式f(x)<x即x|x-2|<x,显然x≠0,当x>0时,原不等式可化为:|x-2|<1,即-1<x-2<1,
解得 1<x<3.
当x<0时,原不等式可化为:|x-2|>1,即x-2>1 或x-2<-1,求得x<0.
综上得:当a=2时,原不等式的解集为{x|1<x<3 或x<0}.
(Ⅱ)∵对任意的x∈(0,4]都有f(x)<4,即-4<x(x-a)<4,
对任意的x∈(0,4]都有x-
| 4 |
| x |
| 4 |
| x |
设g(x)=x-
| 4 |
| x |
| 4 |
| x |
问题等价于x∈(0,4]时,g(x)max<a<p(x)min.
∵g′(x)=1+
| 4 |
| x2 |
又∵p′(x)=1-
| 4 |
| x2 |
| (x-2)(x+2) |
| x2 |
∴p(x)min=p(2)=4 a∈(3,4).
点评:本题主要考查绝对值不等式的解法,函数的恒成立问题,利用导数研究函数的单调性,体现了分类讨论、转化的数学思想,属于中档题.

练习册系列答案
相关题目
在数列{an}中,已知an=
(c∈R),则对于任意正整数n有( )
| n+c |
| n+1 |
| A、an<an+1 |
| B、an与an+1的大小关系和c有关 |
| C、an>an+1 |
| D、an与an+1的大小关系和n有关 |
 如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,侧面是正方形,∠DAB=60°,E是棱CB的延长线上一点,经过点A、C1、E的平面交棱BB1于点F,B1F=2BF.
如图,直四棱柱ABCD-A1B1C1D1的底面是菱形,侧面是正方形,∠DAB=60°,E是棱CB的延长线上一点,经过点A、C1、E的平面交棱BB1于点F,B1F=2BF.