题目内容
已知二次函数f（x）=ax2+bx+c的导数是f′（x）=2x-1，且f（1）=2，求二次函数的解析式．
考点：函数解析式的求解及常用方法,二次函数的性质
专题：函数的性质及应用
分析：求出f（x）的导数f′（x），得出a、b的值，再根据f（1）=2，求出c的值即可．
解答：
解：∵二次函数f（x）=ax2+bx+c的导数是f′（x）=2x-1，
∴2ax+b=2x-1，
解得a=1，b=-1；
又∵f（1）=2，
∴a+b+c=2，
解得c=2；
∴二次函数f（x）的解析式为f（x）=x2-x+2．
∴2ax+b=2x-1，
解得a=1，b=-1；
又∵f（1）=2，
∴a+b+c=2，
解得c=2；
∴二次函数f（x）的解析式为f（x）=x2-x+2．
点评：本题考查了求二次函数的解析式的应用问题，是基础题目．
练习册系列答案
阅读快车系列答案
相关题目
若
（2x+
）dx=3+ln2，且a＞1，则a 的值为（ ）
| ∫ | a 1 |
| 1 |
| x |
| A、6 | B、4 | C、3 | D、2 |
在数列{an}中，已知an=
（c∈R），则对于任意正整数n有（ ）
| n+c |
| n+1 |
| A、an＜an+1 |
| B、an与an+1的大小关系和c有关 |
| C、an＞an+1 |
| D、an与an+1的大小关系和n有关 |
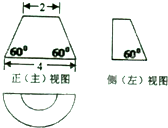
如题图所示为某空间几何体的三视图，则该几何体的表面积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|