题目内容
甲、乙两个工人每人加工一个零件,加工为一等品的概率分别为
和
,两个零件是否被加工为一等品互相独立,则这两个工人加工的两个零件中至少有一个一等品的概率为( )
| 2 |
| 3 |
| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:相互独立事件的概率乘法公式
专题:计算题,概率与统计
分析:利用了对立事件的概率公式,即可得出结论.
解答:
解:分别记甲、乙两个工人加工一个零件为一等品的事件为A,B,则由已知可得P(A)=
,P(B)=
,且A,B相互独立,
由对立事件的概率公式可得,这两个工人加工的两个零件中至少有一个一等品的概率为1-(1-
)(1-
)=
.
故选:A.
| 2 |
| 3 |
| 3 |
| 4 |
由对立事件的概率公式可得,这两个工人加工的两个零件中至少有一个一等品的概率为1-(1-
| 2 |
| 3 |
| 3 |
| 4 |
| 11 |
| 12 |
故选:A.
点评:本题主要考查了相互独立事件的概率公式的求解:若A,B相互独立,则P(AB)=P(A)P(B);还利用了对立事件的概率公式,要注意该方法在解决概率问题时,若正面情况较多时,可以利用此方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
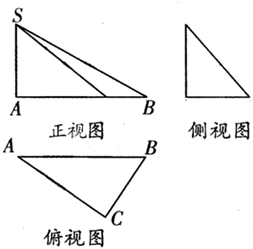 已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )
已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )| A、①② | B、①③ | C、② | D、① |
某几何体的三视图如图所示,则该几何体的体积是( )
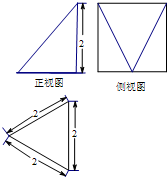

A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
设实数x,y满足约束条件
,则u=
的取值范围是( )
|
| 2x+y |
| x+2y |
A、[
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
设i是虚数单位,则复数z=(
)2013=( )
| 1+i |
| 1-i |
| A、-1 | B、1 | C、-i | D、i |