题目内容
设定点P在圆周x2+y2=1上,若Q,R在x2+y2=1的内部或圆周上,且△PQR为边长是
的正三角形,则OQ2+OR2最大值为 .
| ||
| 2 |
考点:点到直线的距离公式
专题:平面向量及应用
分析:根据题意判断出圆心O在∠QPR内.利用向量减法的几何意义表示
=
-
,
=
-
,则
2+
2=(
-
)2+(
-
)2,根据数量积的运算化简,并根据三角函数的性质之求其最大值即可.
| OQ |
| OQ |
| OP |
| OR |
| OR |
| OP |
| OQ |
| OR |
| OQ |
| OP |
| OR |
| OP |
解答:
解∵P在圆周x2+y2=1上,△PQR为边长是
的正三角形,Q,R在x2+y2=1的内部或圆周上,
∴圆心O在∠QPR内.
∴
=
-
,
=
-
,
∴
2+
2=(
-
)2+(
-
)2
=2
2+
2+
2-2
•
-2
•
=
-2|
||
|cos∠OPQ-2|
||
|cos∠OPR
=
-
(cos∠OPQ+cos∠OPR)
=
-2
cos(
)•cos(
)
=
-2
cos30°cos(
)
≤
-3=
•
故答案为:
.
| ||
| 2 |
∴圆心O在∠QPR内.
∴
| OQ |
| OQ |
| OP |
| OR |
| OR |
| OP |
∴
| OQ |
| OR |
| OQ |
| OP |
| OR |
| OP |
=2
| OP |
| PQ |
| PR |
| OP |
| PQ |
| OP |
| PR |
=
| 7 |
| 2 |
| OP |
| PQ |
| OP |
| PR |
=
| 7 |
| 2 |
| 3 |
=
| 7 |
| 2 |
| 3 |
| ∠OPQ+∠OPR |
| 2 |
| ∠OPQ-∠OPR |
| 2 |
=
| 7 |
| 2 |
| 3 |
| ∠OPQ-∠OPR |
| 2 |
≤
| 7 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查向量减法,数量积运算,以及三角恒变换和三角函数性质的应用,属于中档题.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
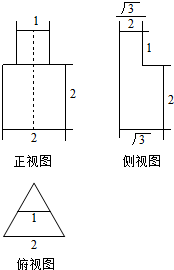

A、3
| ||||
B、
| ||||
C、
| ||||
D、
|
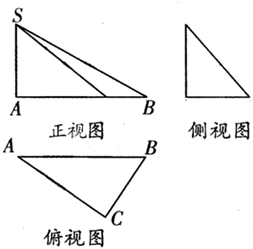 已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )
已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )| A、①② | B、①③ | C、② | D、① |
某几何体的三视图如图所示,则该几何体的体积是( )
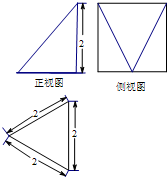

A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
