题目内容
13.向量$\overrightarrow m=({\sqrt{3}sin\frac{x}{4},1}),\overrightarrow n=({cos\frac{x}{4},{{cos}^2}\frac{x}{4}})$,记$f(x)=\overrightarrow m•\overrightarrow n$.(1)若f(x)=1,求$cos({x+\frac{π}{3}})$的值;
(2)在锐角△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求f(2A)的取值范围.
分析 (1)利用数量积运算、两角和差的正弦公式、倍角公式即可得出;
(2)由(2a-c)cosB=bcosC,利用正弦定理可得:2sinAcosB-sinCcosB=sinBcosC,利用两角和的正弦公式和三角形内角和定理可得B=$\frac{π}{3}$,再利用△ABC是锐角三角形求出A的范围,根据正弦函数的性质即可求出
解答 解:(1)记$f(x)=\overrightarrow m•\overrightarrow n$=$\sqrt{3}$sin$\frac{x}{4}$cos$\frac{x}{4}$+cos2$\frac{x}{4}$
=$\frac{\sqrt{3}}{2}$sin$\frac{x}{2}$+$\frac{1}{2}$cos$\frac{x}{2}$+$\frac{1}{2}$=sin($\frac{x}{2}$+$\frac{π}{6}$)+$\frac{1}{2}$,
由f(x)=1,得sin($\frac{x}{2}$+$\frac{π}{6}$)=$\frac{1}{2}$,
∴cos(x+$\frac{π}{3}$)=1-2sin2($\frac{x}{2}$+$\frac{π}{6}$)=$\frac{1}{2}$;
(2)∵(2a-c)cosB=bcosC,
∴由正弦定理得:(2sinA-sinC)cosB=sinBcosC,
∴2sinAcosB-sinCcosB=sinBcosC,又sin(B+C)=sinA,
∴2sinAcosB=sinBcosC+cosBsinC=sin(B+C)=sinA,
∵sinA≠0,∴cosB=$\frac{1}{2}$,
又B为锐角,∴B=$\frac{π}{3}$,
则A+C=$\frac{2π}{3}$,
∴A=$\frac{2}{3}$π-C,
∵0<A<$\frac{π}{2}$,
∴$\frac{π}{6}$<A<$\frac{π}{2}$,
∴$\frac{π}{3}$<A+$\frac{π}{6}$<$\frac{2π}{3}$,
∴$\frac{\sqrt{3}}{2}$<sin(A+$\frac{π}{6}$)≤1,
∵f(2A)=sin(A+$\frac{π}{6}$)+$\frac{1}{2}$
∴f(2A)的取值范围是($\frac{\sqrt{3}+1}{2}$,$\frac{3}{2}$].
点评 本题综合考查了数量积运算、两角和差的正弦公式、倍角公式、正弦定理、两角和的正弦公式和三角形内角和定理、锐角三角形的意义、正弦函数的单调性等基础知识与基本技能方法,考查了综合解决问题的能力,属于中档题.

| A. | $({3,\frac{201}{10}})$ | B. | $({1,\frac{181}{10}})$ | C. | $({2\sqrt{2},+∞})$ | D. | $({2\sqrt{2}-2,+∞})$ |
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 9 |
| A. | $\frac{{\sqrt{3}}}{15}$ | B. | $\frac{{\sqrt{3}}}{16}$ | C. | $\frac{{\sqrt{2}}}{16}$ | D. | $\frac{{\sqrt{2}}}{14}$ |
| A. | [-1,$\frac{1}{2}$] | B. | [-$\frac{1}{4}$,$\frac{1}{2}$] | C. | [-$\frac{5}{3}$,+∞) | D. | (-∞,-$\frac{5}{3}$] |
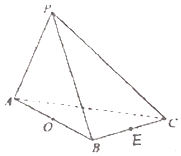 在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.
在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.