题目内容
5.已知定义在R上的函数f(x)=|x+a|+|x|.(Ⅰ)当a=1时,解不等式f(x)≥2;
(Ⅱ)若存在x∈R,使得f(x)<2恒成立,求a的取值范围.
分析 (Ⅰ)当a=1时,化简f(x)=|x+1|+|x|.通关当x≥1,当0<x<1,当x≤0,分别求解不等式的解集即可.(Ⅱ)若存在x∈R,使得f(x)<2恒成立,则f(x)在R上最小值应小于2.利用绝对值的几何意义,转化求解即可.
解答 解:(Ⅰ)当a=1时,f(x)=|x+1|+|x|.
当x≥1,得f(x)=2x-1,由f(x)≥2得x≥$\frac{3}{2}$,此时x$≥\frac{3}{2}$;
当0<x<1,得f(x)=1,此时显然f(x)≥2无解;
当x≤0,得f(x)=1-2x,由f(x)≥2得x$≤-\frac{1}{2}$,此时x$≤-\frac{1}{2}$.
综上,不等式f(x)≥2的解集为:$(-∞,-\frac{1}{2}]∪[\frac{3}{2},+∞)$.
(Ⅱ)若存在x∈R,使得f(x)<2恒成立,则f(x)在R上最小值应小于2.
由绝对值不等式得|x-a|+|x|≥|x-a-x|=|a|,则|a|<2,解得-2<a<2,
从而a的取值范围为:(-2,2).
点评 本题考查函数恒成立条件的应用,绝对值不等式的解法,几何意义的应用,考查计算能力.

练习册系列答案
 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
13.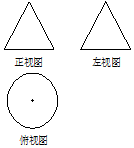 如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )
如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )
 如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )
如图,一个空间几何体正视图与左视图为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的表面积为( )| A. | π | B. | 3π | C. | 2π | D. | $π+\sqrt{3}$ |
10.已知A、B、C、D四点共线,$α∈(\frac{π}{2},π)$,且向量$\overrightarrow{AB}=(tanα,1)$,$\overrightarrow{CD}=(3tan2α,-2)$,则$tan(2α-\frac{π}{4})$等于( )
| A. | $-\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | -7 | D. | 7 |
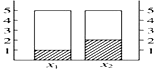
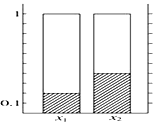
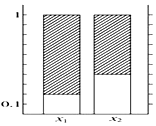
 根据下面列联表作出的条形图中正确的有( )
根据下面列联表作出的条形图中正确的有( )