题目内容
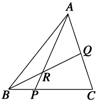
如图所示，P、Q分别在BC和AC上，BP：CP=2：5，CQ：QA=3：4，则
（ ）
| AR |
| RP |
| A、3：14 | B、14：3 |
| C、17：3 | D、17：14 |
考点：相似三角形的性质
专题：选作题,立体几何
分析：过Q点作QM∥AP交BC于M，则
=
=
，由BP：CP=2：5，可得BP：PM=7：10，即可得出结论．
| CM |
| MP |
| CQ |
| QA |
| 3 |
| 4 |
解答：
解：过Q点作QM∥AP交BC于M，则
=
=
，
又∵BP：CP=2：5，∴BP：PM=7：10．
∴RP：QM=BP：BM=7：17，
又QM：AP=CQ：AC=3：7，
∴RP：AP=3：17，∴AR：RP=14：3．
故选：B．
解：过Q点作QM∥AP交BC于M，则| CM |
| MP |
| CQ |
| QA |
| 3 |
| 4 |
又∵BP：CP=2：5，∴BP：PM=7：10．
∴RP：QM=BP：BM=7：17，
又QM：AP=CQ：AC=3：7，
∴RP：AP=3：17，∴AR：RP=14：3．
故选：B．
点评：本题考查相似三角形的性质，考查学生的计算能力，难度中等．
练习册系列答案
相关题目
某程序框图如图所示，该程序运行后输出S的值是（ ）
| A、8 | B、10 | C、31 | D、63 |
函数f（x）=ln（x+1）-
+1的零点所在的大致区间是（ ）
| 2 |
| x |
| A、（0，1） |
| B、（1，2） |
| C、（2，e） |
| D、（3，4） |
经过两点A（4，2y+1），B（2，-3）的直线的斜率为-1，则y等于（ ）
| A、-1 | B、-3 | C、0 | D、2 |
一个正三棱柱的三视图如图所示，则这个正三棱柱的高和底面边长分别为（ ）
A、1，
| ||
B、
| ||
| C、2，1 | ||
| D、1，2 |
若ak=ak（k=1，2，…，2n），bk=a2k（k=1，2，…，n），且数列{ak}的所有项的和为S，则数列{bk}的所有项和S′=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
观察下面的演绎推理过程，判断正确的是（ ）
大前提：若直线a⊥直线 l，且直线b⊥直线 l，则a∥b．
小前提：正方体 ABCD-A1B1C1D1中，A1B1⊥AA1．且AD⊥AA1
结论：A1B1∥AD．
大前提：若直线a⊥直线 l，且直线b⊥直线 l，则a∥b．
小前提：正方体 ABCD-A1B1C1D1中，A1B1⊥AA1．且AD⊥AA1
结论：A1B1∥AD．
| A、推理正确 |
| B、大前提出错导致推理错误 |
| C、小前提出错导致推理错误 |
| D、仅结论错误 |