题目内容
已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）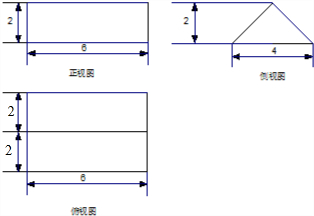
| A、12cm3 | ||
| B、24cm3 | ||
C、
| ||
| D、40cm3 |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：判断三视图复原的几何体的形状，利用三视图的数据求解几何体的体积即可．
解答：
解：由三视图可知几何体是放倒是三棱柱，底面三角形是底边长为4，高为2的等腰三角形，棱柱的高为6．
所求几何体的体积为：
×4×2×6=24（cm3）．
故选：B．
所求几何体的体积为：
| 1 |
| 2 |
故选：B．
点评：本题考查三视图复原几何体的方法，几何体的体积的求法，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
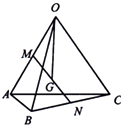已知空间四边形OABC，M，N分别是OA，BC的中点，点G是线段MN的中点，设| OG |
| OA |
| OB |
| OC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知数列{an}为等差数列，a5=5，d=1；数列{bn}为等比数列，b4=16，q=2．
（1）求数列{an}、{bn}的通项公式an、bn；
（2）设cn=an+bn，求数列{cn}的前n项和为Tn．
（1）求数列{an}、{bn}的通项公式an、bn；
（2）设cn=an+bn，求数列{cn}的前n项和为Tn．
y=Asin（ωx+φ）的曲线最高点为（2，
），离它最近的一个最低点是（10，-
），则它的解析式为（ ）
| 2 |
| 2 |
A、f（x）=
| ||||||
B、f（x）=
| ||||||
C、f(x)=
| ||||||
D、f(x)=-
|