题目内容
5.已知M是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左支上一点,A、F分别为双曲线的右顶点和左焦点,且△MAF为等边三角形,则双曲线C的离心率为( )| A. | 2 | B. | 4 | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |
分析 求出M的坐标,利用双曲线的第二定义,列出方程,即可求出双曲线C的离心率.
解答 解:由题意,A(-a,0),F(c,0),△MAF为等边三角形,
则M($\frac{c-a}{2}$,$\frac{\sqrt{3}(c+a)}{2}$),
由双曲线的定义可得$\frac{c+a}{\frac{c-a}{2}-\frac{{a}^{2}}{2}}$=$\frac{c}{a}$
∴c2-3ac-4a2=0,
∴e2-3e-4=0,
∴e=4.
故选:B.
点评 本题考查双曲线C的离心率,考查双曲线的第二定义,正确运用双曲线的第二定义是关键.

练习册系列答案
相关题目
13.“a=-1”是“直线x+ay=1与直线ax+y=5平行”的( )条件.
| A. | 充分但不必要 | B. | 必要但不充分 | ||
| C. | 充分 | D. | 既不充分也不必要 |
15.若?x∈(0,+∞),不等式ax-lnx>0恒成立,则a的取值范围是( )
| A. | (-∞,$\frac{1}{e}$] | B. | (-∞,e] | C. | $({\frac{1}{e},+∞})$ | D. | (e,+∞) |
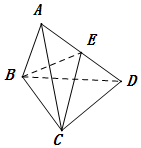 如图所示,△ABC和△BCD都是正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.
如图所示,△ABC和△BCD都是正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点. 如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,
如图,三角形PDC所在的平面与长方形ABCD所在的平面垂直,