题目内容
3.某几何体的三视图如图所示,若此几何体的表面积为(4+2$\sqrt{2}$)π+8,则底面半圆的半径r等于( )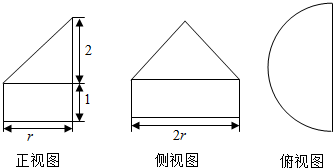
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
分析 由已知中的三视图可得:该几何体是一个以俯视图为底面的半圆柱与半圆锥的组合体,计算其表面积,进而可得答案.
解答 解:由已知中的三视图可得,该几何体是一个半圆柱与半圆锥的组合体,
设底面半圆的半径为r,
则几何体的表面S=$\frac{1}{2}{πr}^{2}$+(2r×1)+($\frac{1}{2}$×2r×2)+(πr×1)+$\frac{1}{2}$πr$\sqrt{{r}^{2}+{2}^{2}}$=(4+2$\sqrt{2}$)π+8,
解得:r=2,
故选:C
点评 本题考查的知识点是由三视图,求体积和表面积,根据已知的三视图,判断几何体的形状是解答的关键.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
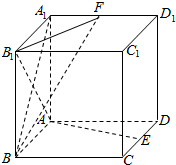 如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是CD、A1D1中点.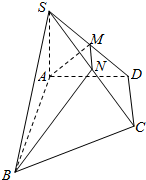 如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,CD=DA=a,AB=2a,SA⊥平面ABCD,且SA=a
如图,在直角梯形ABCD中,∠BAD=∠ADC=90°,CD=DA=a,AB=2a,SA⊥平面ABCD,且SA=a