题目内容
13.有如下四个论断:(1)y=f(x)的定义域为R;
(2)y=f(x)在[3,+∞)上为减函数;
(3)y=f(x)在(-∞,3)上为增函数;
(4)f(1+x)=f(5-x).
以其中三个论断作为条件,余下一个论断作为结论,写出你认为正确的一个命题若y=f(x)的定义域为R,且在[3,+∞)上为减函数,f(1+x)=f(5-x),则y=f(x)在(-∞,3)上是增函数.
分析 由(4)可知f(x)的对称轴为x=3,故f(x)在(-∞,3)和[3,+∞)上的单调性相反,于是由(1)(2)(4)可推出(3),或者由(1)(3)(4)推出(2).
解答 解:由(4)可知f(x)的对称轴为x=3,故f(x)在(-∞,3)和[3,+∞)上的单调性相反.于是由(1)(2)(4)可推出(3),或者由(1)(3)(4)推出(2).
故答案为:若y=f(x)的定义域为R,且在[3,+∞)上为减函数,f(1+x)=f(5-x),则y=f(x)在(-∞,3)上是增函数
点评 本题考查了抽象函数的对称性与单调性,属于中档题.

练习册系列答案
相关题目
3.某几何体的三视图如图所示,若此几何体的表面积为(4+2$\sqrt{2}$)π+8,则底面半圆的半径r等于( )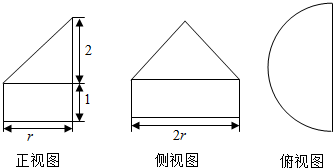

| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
4.在△ABC中,角A为钝角,AB=3,$\overrightarrow{BC}$•$\overrightarrow{BA}$=12,当角C最大时,△ABC的面积等于( )
| A. | 2 | B. | 3 | C. | 5 | D. | $\frac{15}{2}$ |
6.已知函数f(x)=$\sqrt{3}$sinωx+cosωx(ω>0)的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,把函数f(x)的图象沿x轴向右平移$\frac{π}{6}$个单位,得到函数g(x)的图象.若在区间[0,π]上随机取一个数x,则事件“g(x)≥1”发生的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{2}{3}$ |
