题目内容
12.已知直线2x-y-2=0与x、y轴分别交A、B两点,点P在抛物线y=4x2上,试求△PAB面积的最小值.分析 通过三角形的面积公式可知当点P到直线AB的距离最小时面积最小,求出与直线2x-y-2=0平行且为抛物线的切线的直线方程,进而利用两直线间的距离公式及面积公式计算即得结论.
解答 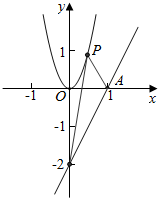 解:依题意,A(1,0),B(0,-2),
解:依题意,A(1,0),B(0,-2),
设与直线2x-y-2=0平行且与抛物线相切的直线l方程为:2x-y-t=0,
联立直线l与抛物线方程,消去y得:4x2-2x+t=0,
则△=4-16t=0,即t=$\frac{1}{4}$,
∵直线2x-y-2=0与直线l之间的距离d=$\frac{2-\frac{1}{4}}{\sqrt{4+1}}$=$\frac{7\sqrt{5}}{20}$,
∴Smin=$\frac{1}{2}$|AB|d=$\frac{1}{2}$•$\sqrt{1+4}$•$\frac{7\sqrt{5}}{20}$=$\frac{7}{8}$.
点评 本题考查直线与圆锥曲线的关系,考查运算求解能力,数形结合是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
3.某几何体的三视图如图所示,若此几何体的表面积为(4+2$\sqrt{2}$)π+8,则底面半圆的半径r等于( )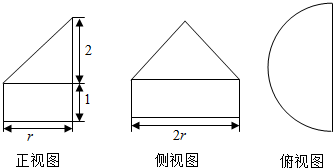

| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
20.执行下列程序框图,则输出结果为( )


| A. | 413 | B. | 404 | C. | 397 | D. | 407 |
17.如图程序框图表示的算法是:求1+2+3+4+…+n>20时n的最小值,则输出框中应填( )


| A. | i | B. | i+1 | C. | i-1 | D. | n |
4.在△ABC中,角A为钝角,AB=3,$\overrightarrow{BC}$•$\overrightarrow{BA}$=12,当角C最大时,△ABC的面积等于( )
| A. | 2 | B. | 3 | C. | 5 | D. | $\frac{15}{2}$ |
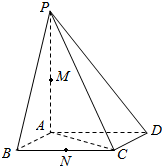 四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.
四棱锥P-ABCD中,PA⊥平面ABCD,ABCD为正方形,AB=PA=2,M,N分别为PA,PB的中点,则MD与AN所成角的余弦值为$\frac{2}{5}$.