题目内容

14．甲、乙两人从4门课程中各选修2门．则不同的选法共有36种，2人所选课程至少有一门相同的概率为$\frac{5}{6}$．

分析 利用组合知识，对立事件的概率公式，即可求解．

解答 解：甲、乙两人从4门课程中各选修2门．则不同的选法共有${C}_{4}^{2}{C}_{4}^{2}$=36种；
2人所选课程至少有一门相同，有36-${C}_{4}^{2}$=30种，∴2人所选课程至少有一门相同的概率为$\frac{30}{36}$=$\frac{5}{6}$，
故答案为36；$\frac{5}{6}$．

点评 本题考查组合知识，对立事件的概率公式，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
2．已知O为坐标原点，F1，F2是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右焦点，双曲线C上一点P满足（$\overrightarrow{OP}$+$\overrightarrow{O{F}_{2}}$）•$\overrightarrow{{F}_{2}P}$=0，且|$\overrightarrow{P{F}_{1}}$|•|$\overrightarrow{P{F}_{2}}$|=2a2，则双曲线C的渐近线方程为（　　）
A．y=±xB．y=±$\sqrt{2}$xC．y=±$\sqrt{3}$xD．y=±2x
5．已知实数x，y满足$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$，则目标函数z=2x-y的最大值为（　　）
A．-3B．$\frac{1}{2}$C．5D．6
2．点P从点（-1，0）出发，沿单位圆x2+y2=1顺时针方向运动$\frac{π}{3}$弧长到达Q点，则Q点的坐标为（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）．
9．设过抛物线y2=4x的焦点F的直线l交抛物线于点A，B，若以AB为直径的圆过点P（-1，2），且与x轴交于M（m，0），N（n，0）两点，则mn=（　　）
A．3B．2C．-3D．-2
19．对于任意实数x，符号[x]表示x的整数部分，即[x]是不超过x的最大整数，例如[2]=2，[2.1]=2，[-2.2]=-3，这个函数[x]叫做“取整函数”，它在数学本身和生产实践中有广泛的应用．已知函数f（x）（x∈R）满足f（x）=f（2-x），且当x≥1时，f（x）=log2x，那么[f（-16）]+[f（-15）]+…+[f（15）]+[f（16）]的值为84．
6．正方体ABCD-A1B1C1D1中与AD1垂直的平面是（　　）
A．平面DD1C1CB．平面A1DBC．平面A1B1C1D1D．平面A1DB1
3．运行图中的程序框图，若输出的结果为57，则判断框内的条件应为（　　）
A．k＞4？B．k≤5？C．k＞3？D．k≤4？
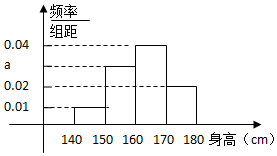4．某中学对高三年级进行身高统计，测量随机抽取的20名学生的身高，其频率分布直方图如图（单位：cm）
（1）求a的值
（2）根据频率分布直方图，求出这20名学生身高中位数的估计值和平均数的估计值．
（3）在身高为140-160的学生中任选2个，求至少有一人的身高在150-160之间的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网