设a∈Z.且0≤a≤13.若512015+a能被13整除.则a=1．题目和参考答案——青夏教育精英家教网—

题目内容

9．设a∈Z，且0≤a≤13，若51²⁰¹⁵+a能被13整除，则a=1．

分析根据51²⁰¹⁵+a=（52-1）²⁰¹⁵+a，把（52-1）²⁰¹⁵+a 按照二项式定理展开，结合题意可得-1+a能被13整除，由此求得a的范围．

解答解：∵51²⁰¹⁵+a=（52-1）²⁰¹⁵+a
=-C₂₀₁₅⁰•52²⁰¹⁵+C₂₀₁₅¹•52²⁰¹⁴-C₂₀₁₅²•52²⁰¹³+…-C₂₀₁₅²⁰¹⁴•52¹-1+a
能被13整除，0≤a＜13，
故-1+a=-1+a能被13整除，故a=1，
故答案为：1．

点评本题主要考查二项式定理的应用，二项式展开式的通项公式，体现了转化的数学思想，属于中档题．

练习册系列答案

小学毕业升学总复习夺冠小状元系列答案

模拟试卷及真题精选系列答案

新课标同步训练系列答案

一线名师口算应用题天天练一本全系列答案

相关题目

,若,则的值等于（）

A． B． C． D．

20．已知直线l的极坐标方程为ρsin（θ+$\frac{π}{3}$）=$\sqrt{3}$，曲线C的参数方程为$\left\{\begin{array}{l}{x=2cosφ}\\{y=sinφ}\end{array}\right.$．（φ为参数）
（1）写出直线l的直角坐标方程和曲线C的普通方程；
（2）求直线l被曲线C截得的弦长．

17．若全集U=R．A={x|1≤x≤5}．B={x|5≤x≤10}．则∁_U（A∩B）=（　　）

4．已知椭圆$M：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率是$\frac{{\sqrt{2}}}{2}$，上顶点B是抛物线x²=4y的焦点．
（Ⅰ）求椭圆M的标准方程；
（Ⅱ）若P、Q是椭圆M上的两个动点，且OP⊥OQ（O是坐标原点），由点O作OR⊥PQ于R，试求点R的轨迹方程．

14．设函数f（x）=sin²（x+$\frac{π}{4}$）-cos²（x+$\frac{π}{4}$）（x∈R），则函数f（x）是（　　）

	A．	最小正周期为π的奇函数		B．	最小正周期为π的偶函数
	C．	最小正周期为$\frac{π}{2}$的奇函数		D．	最小正周期为$\frac{π}{2}$的偶函数

1．

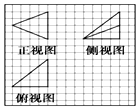如图，方格纸上正方形小格的边长为1，图中粗实线画出的是由一个正方体截得的一个几何体的三视图，则该几何体的体积为（　　）

18．已知曲线C的极坐标方程是ρ-2cosθ-4sinθ=0，以极点为在平面直角坐标系的原点，极轴为x轴的正半轴建立平面直角坐标系xoy，直线的参数方程为$\left\{\begin{array}{l}x=\frac{{\sqrt{3}}}{2}t\\ y=1+\frac{1}{2}t\end{array}\right.$（t为参数）．
（1）将曲线C的极坐标方程化为直角坐标方程，将直线l的参数方程化为普通方程；
（2）若直线l与曲线C相交于A，B两点，与y轴交于点M，求（|MA|+|MB|）²的值．

19．曲线y=x²的一种参数方程是（　　）

A．

$\left\{{\begin{array}{l}{x={t^2}}\\{y={t^4}}\end{array}}\right.$

B．

$\left\{{\begin{array}{l}{x=sint}\\{y={{sin}^2}t}\end{array}}\right.$

C．

$\left\{{\begin{array}{l}{x=\sqrt{t}}\\{y=t}\end{array}}\right.$

D．

$\left\{{\begin{array}{l}{x=t}\\{y={t^2}}\end{array}}\right.$

试题分类