题目内容
6.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$),x=-$\frac{π}{4}$为f(x)的零点,x=$\frac{π}{4}$为y=f(x)图象的对称轴,且f(x)在($\frac{π}{18}$,$\frac{5π}{36}$)上单调,则ω的最大值是( )| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
分析 根据已知可得ω为正奇数,且ω≤12,结合x=-$\frac{π}{4}$为f(x)的零点,x=$\frac{π}{4}$为y=f(x)图象的对称轴,求出满足条件的解析式,并结合f(x)在($\frac{π}{18}$,$\frac{5π}{36}$)上单调,可得ω的最大值.
解答 解:∵x=-$\frac{π}{4}$为f(x)的零点,x=$\frac{π}{4}$为y=f(x)图象的对称轴,
∴$\frac{2n+1}{4}$•T=$\frac{π}{2}$,即 $\frac{2n+1}{4}$•$\frac{2π}{ω}$=$\frac{π}{2}$,(n∈N)
即ω=2n+1,(n∈N)
即ω为正奇数,
∵f(x)在($\frac{π}{18}$,$\frac{5π}{36}$)上单调,则$\frac{5π}{36}$-$\frac{π}{18}$=$\frac{π}{12}$≤$\frac{T}{2}$,
即T=$\frac{2π}{ω}$≥$\frac{π}{6}$,解得:ω≤12,
当ω=11时,-$\frac{11π}{4}$+φ=kπ,k∈Z,
∵|φ|≤$\frac{π}{2}$,
∴φ=-$\frac{π}{4}$,
此时f(x)在($\frac{π}{18}$,$\frac{5π}{36}$)不单调,不满足题意;
当ω=9时,-$\frac{9π}{4}$+φ=kπ,k∈Z,
∵|φ|≤$\frac{π}{2}$,
∴φ=$\frac{π}{4}$,
此时f(x)在($\frac{π}{18}$,$\frac{5π}{36}$)单调,满足题意;
故ω的最大值为9,
故选:C.
点评 本题考查的知识点是正弦型函数的图象和性质,本题转化困难,难度较大.

练习册系列答案
相关题目
17.若全集U=R.A={x|1≤x≤5}.B={x|5≤x≤10}.则∁U(A∩B)=( )
| A. | {x|x≠5} | B. | {x|x=5} | C. | {x|x<5} | D. | {x|x>5} |
14.设函数f(x)=sin2(x+$\frac{π}{4}$)-cos2(x+$\frac{π}{4}$)(x∈R),则函数f(x)是( )
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为π的偶函数 | ||
| C. | 最小正周期为$\frac{π}{2}$的奇函数 | D. | 最小正周期为$\frac{π}{2}$的偶函数 |
1.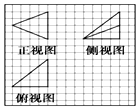 如图,方格纸上正方形小格的边长为1,图中粗实线画出的是由一个正方体截得的一个几何体的三视图,则该几何体的体积为( )
如图,方格纸上正方形小格的边长为1,图中粗实线画出的是由一个正方体截得的一个几何体的三视图,则该几何体的体积为( )
 如图,方格纸上正方形小格的边长为1,图中粗实线画出的是由一个正方体截得的一个几何体的三视图,则该几何体的体积为( )
如图,方格纸上正方形小格的边长为1,图中粗实线画出的是由一个正方体截得的一个几何体的三视图,则该几何体的体积为( )| A. | $\frac{16}{3}$ | B. | $\frac{32}{3}$ | C. | $\frac{64}{3}$ | D. | 32 |
16.下列推理是演绎推理的是( )
| A. | 由 ${a_1}=1,{a_{n+1}}=\frac{a_n}{{1+{a_n}}}$,因为${a_1}=1,{a_2}=\frac{1}{2},{a_3}=\frac{1}{3},{a_4}=\frac{1}{4}$,故有${a_n}=\frac{1}{n}(n∈{N^*})$ | |
| B. | 科学家利用鱼的沉浮原理制造潜艇 | |
| C. | 妲己惑纣王,商灭;西施迷吴王,吴灭;杨贵妃迷唐玄宗,致安史之乱,故曰:“红颜祸水也” | |
| D. | 《论语•学路》篇中说:“名不正,则言不顺;言不顺,则事不成;事不成,则礼乐不兴;礼乐不兴,则刑罚不中;刑罚不中,则民无所措手足;所以,名不正,则民无所措手足”. |
 、
、 , 平面α,
, 平面α,  ∥
∥ ,
,  ∥α, 那么
∥α, 那么 与平面α的关系是( ).
与平面α的关系是( ). ∥α
∥α
 α
α ∥α或
∥α或
 α
α 与α相交
与α相交